Page 270 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 270

τελικά
lim [f(x) g(x)]=(f g)(0)=-6
x x 0
δηλαδή η f g είναι συνεχής στο χ 0=0

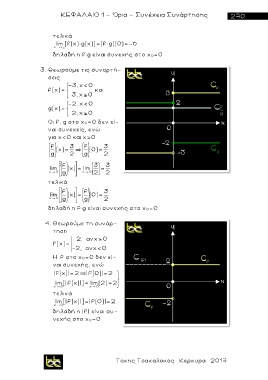
3. Θεωρούμ ε τις συναρτή-
σεις

-3, x<0
f(x)= και
3, x 0

-2, x<0
g(x)=
2, x 0

Oι f, g στο χ 0=0 δεν εί-
ναι συνεχείς, ε ν ώ
για χ<0 και χ 0

f (x)= 3 ~ f (0)= 3
g 2 g 2

f 3 3
lim (x) = lim
x 0 g x 0 2 2

τελικά
f f 3
lim (x) = (0)=
x 0 g g 2

δηλαδή η f g είναι συνεχής στο χ 0=0

4. Θεωρούμε τη συνάρ-
τηση
2, αν χ 0
f(x)=
-2, αν χ 0
Η f στο χ 0=0 δεν ε ί -
ναι συνεχής, ε ν ώ

| f(x)|=2~| f(0)|=2

lim[| f(x)|]= lim(2) 2
x 0 x 0
τελικά

lim[| f(x)|]=| f(0)|=2
x 0
δηλαδή η |f| είναι σ υ -

νεχής στο χ 0=0

Τακης Τσακαλακος Κερκυρα 2017