Page 24 - FORMULARIO TRIGONOMETRIA - GALILEO

Academia
Galileo Formulario de TRIGONOMETRÍA
Para Ingenierías y Ciencias Médicas
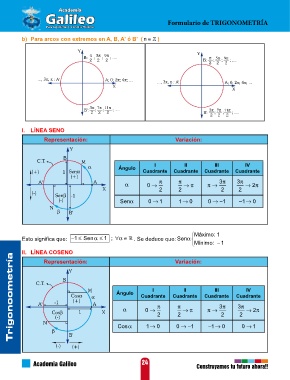
b) Para arcos con extremos en A, B, A' ó B' ( n ∈ )

Y Y
B: π 5π 9π π 5π 9π
; ; ; ....
2 2 2 B: ; ; ; ....
2 2 2
..., 3π, π : A' A; 0; 2; 4; ...π π ..., 3π, π : A' A; 0; 2; 4; ...π π
X
X

3π 7π 11π
B': 2 ; ; ; .... B': 3π 7π 11π
2
2
; ; ; ....
2 2 2
I. LÍNEA SENO
Representación: Variación:
Y
B
C.T. M
α Ángulo I II III IV
(+) 1 Senα Cuadrante Cuadrante Cuadrante Cuadrante
(+)
A' A α 0 → π π → π π → 3 π 3π → 2π
X 2 2 2 2
(-)
Senβ -1
(-) Senα 0 → 1 1→ 0 0 →− 1 −→1 0
N
β B'

 Máximo: 1
Esto significa que: −≤1 Senα ≤ 1 ; ∀ ∈α  . Se deduce que: Senα 
 Mínimo: 1−
II. LÍNEA COSENO Variación:
Trigonoometría C.T. Cosβ B Cosα M α A X Ángulo Cuadrante Cuadrante Cuadrante Cuadrante
Representación:
Y

II
I
III
IV
(+)
-1
A'
3
3π
π
π
π
α
0 →
→
π →
2π
→
π
1
2
2
2
2
(-)
N
β
(-) B' (+) Cosα 1→ 0 0 →− 1 −→1 0 0 → 1
Academia Galileo 24 Construyamos tu futuro ahora!!