Page 36 - FORMULARIO TRIGONOMETRIA - GALILEO
P. 36
Academia
Galileo Formulario de TRIGONOMETRÍA
Para Ingenierías y Ciencias Médicas
ANÁLISIS DE LAS FUNCIONES TRIGONOMÉTRICAS
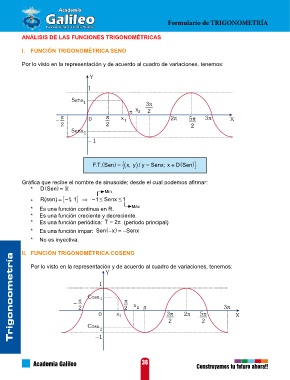
I. FUNCIÓN TRIGONOMÉTRICA SENO
Por lo visto en la representación y de acuerdo al cuadro de variaciones, tenemos:
Y
1
Senx 1 3π
π x 2 2
− π 0 π x 1 2π 5π 3π X
2 2 2
Senx 2
− 1
D Sen)}
FT Sen..( ) = x y, ( { / ) y = Senx x; ∈ (
Gráfica que recibe el nombre de sinusoide; desde el cual podemos afirmar:
(
* DSen) = Mín
, ] ⇒− ≤1
* Rsen( ) =− [ 11 Senx ≤ 1
* Es una función continua en R. Máx
* Es una función creciente y decreciente.
* Es una función periódica: T = 2π (periodo principal)
* Es una función impar: Sen − ( x) =− Senx
* No es inyectiva.
II. FUNCIÓN TRIGONOMÉTRICA COSENO
Trigonoometría − π Cosx 0 1 1 x 1 π x 2 π 3π 2π 5π 3π X
Por lo visto en la representación y de acuerdo al cuadro de variaciones, tenemos:
Y
2
2
2
2
− 1
Cosx 2
Academia Galileo 36 Construyamos tu futuro ahora!!