Page 37 - FORMULARIO TRIGONOMETRIA - GALILEO

Academia
Galileo
Formulario de TRIGONOMETRÍA
Para Ingenierías y Ciencias Médicas
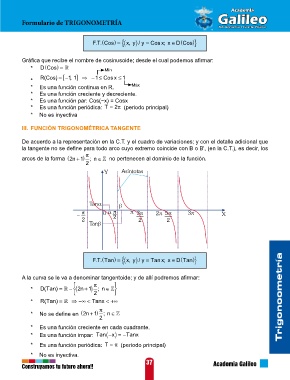
FT.. Cos) = ( { xy, ) / y = Cos x x; ∈ (
D Cos)}
(
Gráfica que recibe el nombre de cosinusoide; desde el cual podemos afirmar:
(
* DCos) =  Mín
, ] ⇒− ≤1
* R(Cos) =− [ 11 Cos x ≤ 1
* Es una función continua en R. Máx
* Es una función creciente y decreciente.
* Es una función par: Cos(−x) = Cosx
* Es una función periódica: T = 2π (periodo principal)
* No es inyectiva

III. FUNCIÓN TRIGONOMÉTRICA TANGENTE

De acuerdo a la representación en la C.T. y el cuadro de variaciones; y con el detalle adicional que
la tangente no se define para todo arco cuyo extremo coincide con B o B', (en la C.T.), es decir, los
π
(
arcos de la forma 2n + ) ; n ∈ no pertenecen al dominio de la función.
1
2
Y Asíntotas

Tanα β
π 0 α π π 3π 2π 5π 3π X
− 2
2 2 2
Tanβ

FT.. Tan) = ( { xy, ) / y = Tan x x; ∈ (
D Tan)}
(
A la curva se le va a denominar tangentoide; y de allí podremos afirmar:
{
* DTan( ) =  − (2 n + ) 1 π 2 ; n ∈ }

* RTan( ) =  ⇒ −∞ < Tanx < +∞ Trigonoometría
π
(
1
* No se define en 2n + ) ; n ∈
2
* Es una función creciente en cada cuadrante.
* Es una función impar: Tan − ( x) =− Tanx
* Es una función periódica: T =π (período principal)
* No es inyectiva.
37 Academia Galileo
Construyamos tu futuro ahora!!