Page 116 - Cambridge+Checkpoint+Mathematics+Coursebook+9

12.2 Solving transformation problems

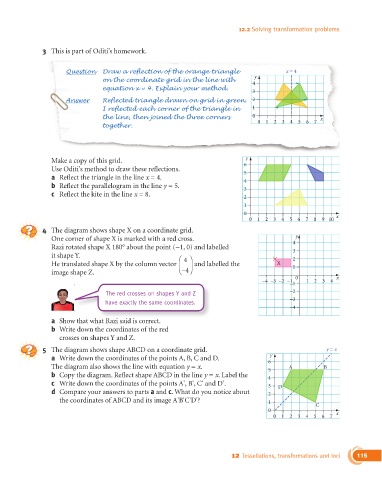
3 This is part of Oditi’s homework.

Question Draw a reflection of the orange triangle x = 4
on the coordinate grid in the line with 4 y
equation x = 4. Explain your method.
3
Answer Reflected triangle drawn on grid in green. 2
I reflected each corner of the triangle in 1
the line, then joined the three corners 0 x
together. 0 1 2 3 4 5 6 7

Make a copy of this grid. y
Use Oditi’s method to draw these reflections. 6

5
a Reflect the triangle in the line x = 4. 4

b Reflect the parallelogram in the line y = 5. 3

c Reflect the kite in the line x = 8. 2
1
0 x
0 1 2 3 4 5 6 7 8 9 10
4 The diagram shows shape X on a coordinate grid.
One corner of shape X is marked with a red cross. 4 y
Razi rotated shape X 180° about the point (−1, 0) and labelled 3
it shape Y.  4  2
He translated shape X by the column vector   and labelled the X 1
image shape Z. −  4
0 x
–4 –3 –2 –1 1 2 3 4
–1
The red crosses on shapes Y and Z –2
–3
have exactly the same coordinates.
–4
a Show that what Razi said is correct.
b Write down the coordinates of the red
crosses on shapes Y and Z.
5 The diagram shows shape ABCD on a coordinate grid. y = x
a Write down the coordinates of the points A, B, C and D. 6 y
The diagram also shows the line with equation y = x. 5 A B

b Copy the diagram. Reflect shape ABCD in the line y = x. Label the 4
c Write down the coordinates of the points A', B', C' and D'. 3 D
d Compare your answers to parts a and c. What do you notice about 2
the coordinates of ABCD and its image A'B'C'D'? 1
C
0
0 1 2 3 4 5 6 7 x

12 Tessellations, transformations and loci 115