Page 495 - Maxwell House

APPENDIX 475

Stokes’ Theorem

Linear Integral of Vector Fields. Practically, the vectors describing electric and magnetic fields
define the force affecting directly or indirectly on charged particle or assemblies of such
particles. As it has been demonstrated in Chapter 1, all EM vectors can be determined through
Lorentz’s force law = Δ + Δ x . If so, we must have the tool to estimate the work

produced by such kind of vector fields. It is known from the classical mechanics that the work
by force can be calculated as
= ∫ () ∘ (A.50)

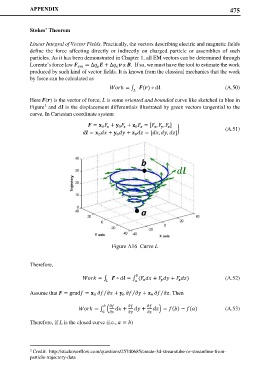
Here () is the vector of force, L is some oriented and bounded curve like sketched in blue in
Figure and is the displacement differentials illustrated by green vectors tangential to the
3
curve. In Cartesian coordinate system

= + + = [ , , ] � (A.51)
0
0
0

= + + = [, , ]
0
0
0

Figure A16 Curve L

Therefore,

= ∫ ∘ = ∫ ( + + ) (A.52)

Assume that = grad = + + . Then
⁄
⁄
⁄
0 0 0

= ∫ � + + � = () − () (A.53)

Therefore, if L is the closed curve (i.e., = )

3 Credit: http://stackoverflow.com/questions/25740685/create-3d-streamtube-or-streamline-from-
particle-trajectory-data