Page 65 - Mechatronics with Experiments

CLOSED LOOP CONTROL 51
y(t) y(kT)

T(s)
ω = 2/T(rad/s)
S
t t 0T 2T.....

ω
ω
|y( j )| |y*(j )|
ω ma x = ω 1 > ω S /2

-ω ω -ω ω ω ω
1 1 1 1 S
Enlarged view

ω * ω S
ω 1
ω * =(ω - ω )
Low freq. alias S 1 High freq. component
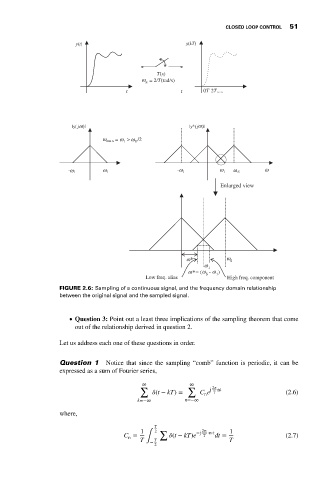
FIGURE 2.6: Sampling of a continuous signal, and the frequency domain relationship
between the original signal and the sampled signal.

Question 3: Point out a least three implications of the sampling theorem that come

out of the relationship derived in question 2.
Let us address each one of these questions in order.

Question 1 Notice that since the sampling “comb” function is periodic, it can be
expressed as a sum of Fourier series,

∞ ∞
∑ ∑ j 2 nt
(t − kT) = C e T (2.6)
n
k=−∞ n=−∞
where,

T
1 2 ∑ −j 2π ⋅n⋅t 1
C = T ∫ T (t − kT)e T dt = T (2.7)
n
−
2