Page 7 - E-Modul Geometri Dasar Segi Banyak

Geometri Dasar Segi Banyak
Geometri Dasar Segi Banyak ii 2
Geometri Dasar Segi Banyak
Geometri Dasar Segi Banyak

Teorema 2.2

Jumlah diagonal suatu segi-n adalah n/2(n-3)

Bukti :

1

Diketahui untuk 1 titik sudut,
dapat ditarik (n-3) diagonal (teorema 1.1)
Maka untuk n titik sudut, dapat ditarik n(n-3) diagonal

2

Jumlah n(n-3) ini harus dibagi dengan 2
Karena tiap-tiap diagonal terhitung 2 kali misalnya
dari A ke C sama dengan C ke A. jadi banyaknya diagonal
suatu segi n adalah n/2(n-3)

Teorema 2.3

Jumlah sudut suatu segi-n adalah (n-2) 180

Bukti :
1
E
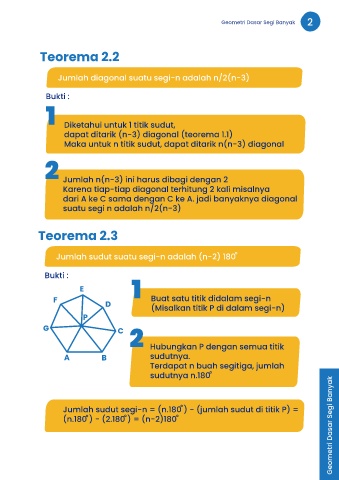
F Buat satu titik didalam segi-n
D
(Misalkan titik P di dalam segi-n)
P
G
C
2 Hubungkan P dengan semua titik

A B sudutnya.
Terdapat n buah segitiga, jumlah
sudutnya n.180
Geometri Dasar Segi Banyak Geometri Dasar Segi Banyak

Jumlah sudut segi-n = (n.180 ) - (jumlah sudut di titik P) =
(n.180 ) - (2.180 ) = (n-2)180