Page 227 - Matematica 1° Sec

Razones trigonométricas Capítulo 12

de ángulo agudo II

RAZÓN TRIGONOMÉTRICA TANGENTE

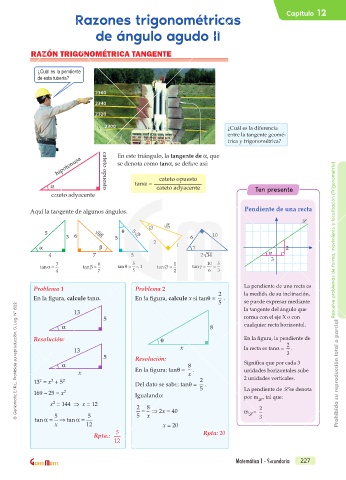
¿Cuál es la pendiente
de esta tubería?

2360
2340
2320

2300 ¿Cuál es la diferencia
entre la tangente geomé-
trica y trigonométrica?

En este triángulo, la tangente de a, que
hipotenusa cateto opuesto se denota como tana, se define así:

cateto opuesto
a tana = cateto adyacente Ten presente
cateto adyacente

Aquí la tangente de algunos ángulos. Pendiente de una recta
L L
 5
5 q 5 10
3 6 85 5 2 6
2 Resuelve problemas de forma, movimiento y localización (Trigonometría)
a b 1 g 2
4 7 5 2 34 a
3
3 6 5 1 10 5
tan α= tanβ= tan θ= = 1 tan∅= tan γ= =
4 7 5 2 6 3

Problema 1 Problema 2 La pendiente de una recta es
2 la medida de su inclinación,
En la figura, calcule tana. En la figura, calcule x si tanq = .
5 se puede expresar mediante
 Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
la tangente del ángulo que
13
5 forma con el eje X o con
a 8 cualquier recta horizontal.

Resolución: q En la figura, la pendiente de
x la recta es tana = 2 .
13 3
5 Resolución:
a 8 Significa que por cada 3
x En la figura: tanq = x . unidades horizontales sube Prohibida su reproducción total o parcial
2
2
13 = x + 5 2 Del dato se sabe: tanq = 2 . 2 unidades verticales.
L

2
169 – 25 = x Igualando: 5 La pendiente de L se denota
por m , tal que:
2
x = 144  x = 12 L L
2 = 8 ⇒ 2 =x 40 2
L L
5 5 5 x m = 3
tan α = ⇒ tan α =
x 12 x = 20
Rpta.: 5 Rpta: 20
12
Matemática 1 - Secundaria 227