Page 228 - Matematica 1° Sec

Razones trigonométricas de ángulo agudo II

RAZÓN TRIGONOMÉTRICA COTANGENTE

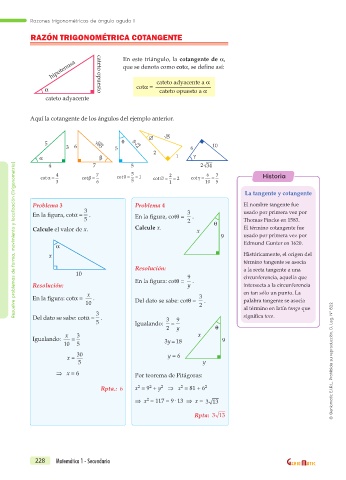
hipotenusa cateto opuesto En este triángulo, la cotangente de a,
que se denota como cota, se define así:

cateto adyacente a a
a cota = cateto opuesto a a
cateto adyacente

Aquí la cotangente de los ángulos del ejemplo anterior.

 5
5 q 5
3 6 85 5 2 6 10
2
a b 1 g
Resuelve problemas de forma, movimiento y localización (Trigonometría)
4 7 5 2 34
4 7 5 2 6 3 Historia
cotα= cotβ= cotθ= = 1 cot∅= = 2 cot γ= =
3 6 5 1 10 5

La tangente y cotangente
Problema 3 Problema 4 El nombre tangente fue
3 3 usado por primera vez por
En la figura, cota = . En la figura, cotq = .
5 2 q Thomas Fincke en 1583.
Calcule el valor de x. Calcule x. x El término cotangente fue
9 usado por primera vez por
a Edmund Gunter en 1620.
x Históricamente, el origen del
término tangente se asocia
Resolución: a la recta tangente a una
10 9 circunferencia, aquella que
En la figura: cotq = .
Resolución: y intersecta a la circunferencia
x en tan sólo un punto. La
En la figura: cota = . Del dato se sabe: cotq = 3 . palabra tangente se asocia
10 2 al término en latín tongo que
3
Del dato se sabe: cota = . 3 9 significa toco.
5 Igualando: =
2 y q
x 3 x
Igualando: = 3y = 18 9
10 5
30 y = 6
x =
5 y  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
⇒ x = 6 Por teorema de Pitágoras:

2
2
2
2
Rpta.: 6 x = 9 + y  x = 81 + 6 2
2

 x = 117 = 9 · 13  x = 313
Rpta:

228 Matemática 1 - Secundaria