Page 148 - Geometria 1° Sec GM

Capítulo 22 Geometría analítica IV

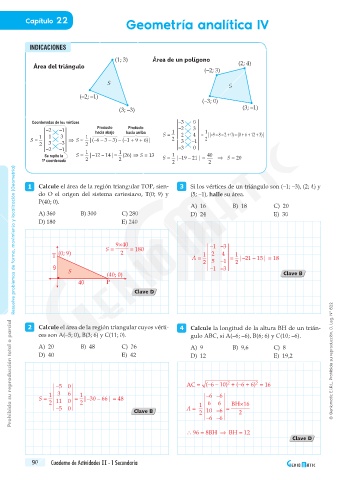
INDICACIONES

(1; 3) Área de un polígono
Área del triángulo (2; 4)
(–2; 3)

S
S
(–2; –1)
(–3; 0)
(3; –3) (3; –1)

Coordenadas de los vértices –3 0
Producto Producto –2 3
–2 –1 hacia abajo hacia arriba 1 1
1 1 3 1 S = 2 4 = |(–9 – 8 – 2 + 0) – (0 + 6 + 12 + 3)|
S = S = |(–6 – 3 – 3) – (–1 + 9 + 6)| 2 3 –1 2
2 3 –3 2
–2 –1 1 1 –3 0
1
Se repite la S = |–12 – 14|= (26) S = 13 S = |–19 – 21| = 40 S = 20
1ª coordenada 2 2 2 2
Resuelve problemas de forma, movimiento y localización (Geometría)

1 Calcule el área de la región triangular TOP, sien- 3 Si los vértices de un triángulo son (–1; –3), (2; 4) y
do O el origen del sistema cartesiano, T(0; 9) y (5; –1), halle su área.
P(40; 0).
A) 16 B) 18 C) 20
A) 360 B) 300 C) 280 D) 24 E) 30
D) 180 E) 240

9×40 –1 –3
S = = 180
1 2
1
T (0; 9) 2 A = 4 = |–21 – 15| = 18
9 2 5 –1 2
–1 –3
S Clave B
(40; 0)
40 P

Clave D

Prohibida su reproducción total o parcia l
2 Calcule el área de la región triangular cuyos vérti- 4 Calcule la longitud de la altura BH de un trián-
ces son A(–5; 0), B(3; 6) y C(11; 0). gulo ABC, si A(–6; –6), B(6; 6) y C(10; –6).
A) 20 B) 48 C) 36 A) 9 B) 9,6 C) 8
D) 40 E) 42 D) 12 E) 19,2  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822

2
2
–5 0 AC = (–6 – 10) + (–6 + 6) = 16
1 3 6 1 –6 –6
S = = |–30 – 66| = 48
2 11 0 2 1 6 6 BH×16
–5 0 Clave B A = 10 –6 = 2
2
–6 –6
\ 96 = 8BH  BH = 12
Clave D

90 Cuaderno de Actividades II - 1 Secundaria