Page 144 - Geometria 1° Sec GM

Capítulo 21 Geometría analítica III

INDICACIONES

(c; d)
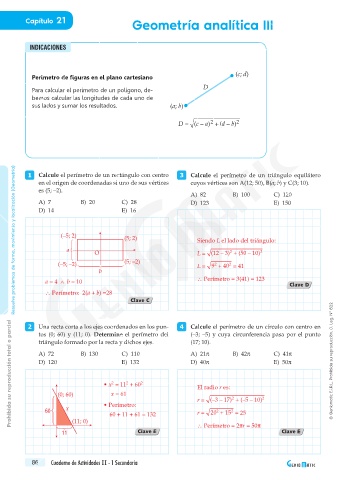
Perímetro de figuras en el plano cartesiano
D
Para calcular el perímetro de un polígono, de-
bemos calcular las longitudes de cada uno de
sus lados y sumar los resultados. (a; b)

D = (c – a) (d – b)

Resuelve problemas de forma, movimiento y localización (Geometría)
1 Calcule el perímetro de un rectángulo con centro 3 Calcule el perímetro de un triángulo equilátero
en el origen de coordenadas si uno de sus vértices cuyos vértices son A(12; 50), B(a; b) y C(3; 10).
es (5; –2).
A) 82 B) 100 C) 120
A) 7 B) 20 C) 28 D) 123 E) 150
D) 14 E) 16

(–5; 2) (5; 2) Siendo L el lado del triángulo:

a
2
2
O L = (12 – 3) + (50 – 10)
(5; –2)
(–5; –2) L = 9 + 40 = 41
2
2
b
a = 4  b = 10 \ Perímetro = 3(41) = 123
Clave D
\ Perímetro: 2(a + b) =28
Clave C

Prohibida su reproducción total o parcia l
2 Una recta corta a los ejes coordenados en los pun- 4 Calcule el perímetro de un círculo con centro en
tos (0; 60) y (11; 0). Determine el perímetro del (–3; –5) y cuya circunferencia pasa por el punto
triángulo formado por la recta y dichos ejes. (17; 10).

A) 72 B) 130 C) 110 A) 21 B) 42 C) 41
D) 120 E) 132 D) 40 E) 50  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822

2
2
• x = 11 + 60 2
El radio r es:
(0; 60) x = 61

2
2
r = (–3 – 17) + (–5 – 10)
x • Perímetro:
2
2
60 60 + 11 + 61 = 132 r = 20 + 15 = 25
(11; 0)
\ Perímetro = 2r = 50
11 Clave E Clave E
86 Cuaderno de Actividades II - 1 Secundaria