Page 145 - Geometria 1° Sec GM

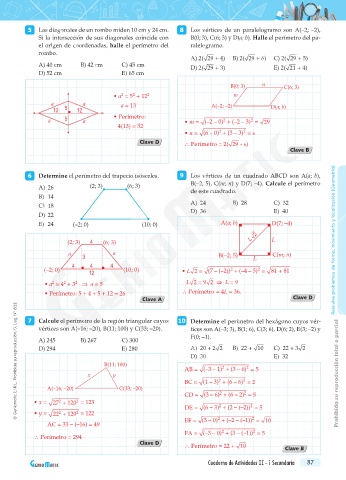
5 Las diagonales de un rombo miden 10 cm y 24 cm. 8 Los vértices de un paralelogramo son A(–2; –2),
Si la intersección de sus diagonales coincide con B(0; 3), C(6; 3) y D(a; b). Halle el perímetro del pa-
el origen de coordenadas, halle el perímetro del ralelogramo.
rombo.
A) 2( 29 + 4) B) 2( 29 + 6) C) 2( 29 + 5)
A) 40 cm B) 42 cm C) 45 cm D) 2( 29 + 3) E) 2( 21 + 4)
D) 52 cm E) 65 cm

B(0; 3) n C(6; 3)
2
2
• a = 5 + 12 2 m
a 5 a a = 13 A(–2; –2) D(a; b)
12 12
5 • Perímetro:
a a • m = (–2 – 0) + (–2 – 3) = 29
2
2
4(13) = 52
2
2
• n = (6 – 0) + (3 – 3) = 6
Clave D \ Perímetro = 2( 29 + 6)
Clave B

6 Determine el perímetro del trapecio isósceles. 9 Los vértices de un cuadrado ABCD son A(a; b),

A) 26 (2; 3) (6; 3) B(–2; 5), C(m; n) y D(7; –4). Calcule el perímetro
de este cuadrado.
B) 14
C) 18 A) 24 B) 28 C) 32
D) 22 D) 36 E) 40
E) 24 (–2; 0) (10; 0) A(a; b) D(7; –4)
L 2
(2; 3) 4 (6; 3) L Resuelve problemas de forma, movimiento y localización (Geometría)

a a B(–2; 5) C(m; n)
3 L
4 4 4
(–2; 0) (10; 0) • L 2 = (7 – (–2)) + (–4 – 5) = 81 + 81
2
2
12
2
2
2
• a = 4 + 3  a = 5 L 2 = 9 2  L = 9
• Perímetro: 5 + 4 + 5 + 12 = 26 \ Perímetro = 4L = 36.
Clave A Clave D
 Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
7 Calcule el perímetro de la región triangular cuyos 10 Determine el perímetro del hexágono cuyos vér-
vértices son A(–16; –20), B(11; 100) y C(33; –20). tices son A(–3; 3), B(1; 6), C(3; 6), D(6; 2), E(3; –2) y
F(0; –1).
A) 245 B) 267 C) 300
D) 294 E) 280 A) 20 + 2 2 B) 22 + 10 C) 22 + 3 2
D) 30 E) 32
B(11; 100)
2
2
AB = (–3 – 1) + (3 – 6) = 5
x y Prohibida su reproducción total o parcial
2
2
BC = (1 – 3) + (6 – 6) = 2
A(–16; –20) C(33; –20)
2
2
CD = (3 – 6) + (6 – 2) = 5
2
2
• x = 27 + 120 = 123
2
2
DE = (6 – 3) + (2 – (–2)) = 5
• y = 22 + 120 = 122
2
2
2
2
EF = (3 – 0) + (–2 – (–1)) = 10
AC = 33 – (–16) = 49
2
2
FA = (–3 – 0) + (3 – (–1)) = 5
\ Perímetro = 294
Clave D \ Perímetro = 22 + 10 Clave B
Cuaderno de Actividades II - 1 Secundaria 87