Page 27 - Trigonometria 1° Sec GM

Razones trigonométricas de ángulo agudo I
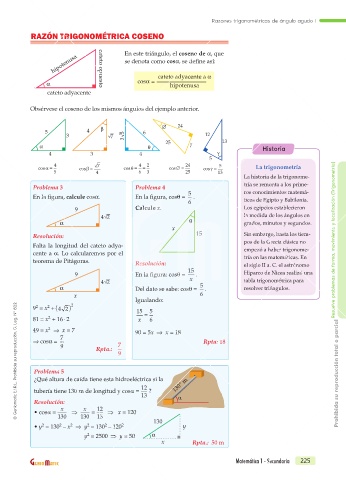
RAZÓN TRIGONOMÉTRICA COSENO

En este triángulo, el coseno de a, que
hipotenusa cateto opuesto se denota como cosa, se define así:

cateto adyacente a a
a cosa = hipotenusa
cateto adyacente

Obsérvese el coseno de los mismos ángulos del ejemplo anterior.

5 4 b 5 6  24
3 7 12
2 13
a q 25 7 Historia
4 3 4 g
5
4 7 4 2 24 5 La trigonometría
cosα= cosβ= cosθ= = cos∅= cos γ=
5 4 6 3 25 13
La historia de la trigonome-
Problema 3 Problema 4 tría se remonta a los prime-
En la figura, calcule cosa. En la figura, cosq = 5 . ros conocimientos matemá-
6 ticos de Egipto y Babilonia.
9 Calcule x. Los egipcios establecieron
4 2 la medida de los ángulos en
a q grados, minutos y segundos.
x
Resolución: 15 Sin embargo, hasta los tiem-
pos de la Grecia clásica no Resuelve problemas de forma, movimiento y localización (Trigonometría)
Falta la longitud del cateto adya-
cente a a. Lo calcularemos por el empezó a haber trigonome-
teorema de Pitágoras. Resolución: tría en las matemáticas. En
el siglo II a. C. el astrónomo
15
9 En la figura: cosq = . Hiparco de Nicea realizó una
4 2 x tabla trigonométrica para
a Del dato se sabe: cosq = 5 . resolver triángulos.
x 6
Igualando:
(
9 = x + 42) 2
 Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
2
2
15 = 5
2

81 = x + 16 ⋅ 2 x 6
2
49 = x  x = 7 90 = 5x  x = 18
7
 cosa = Rpta: 18
9 Rpta.: 7
9
Problema 5 Prohibida su reproducción total o parcial
¿Qué altura de caída tiene esta hidroeléctrica si la
12 130° m
tubería tiene 130 m de longitud y cosa = ?
13 α
Resolución:
x x 12
• cosa = ⇒ = ⇒ x = 120
130 130 13
130
2
2
2
2
2
• y = 130 – x ⇒ y = 130 – 120 2 y
2
y = 2500 ⇒ y = 50
x Rpta.: 50 m
Matemática 1 - Secundaria 225