Page 3 - mathematics

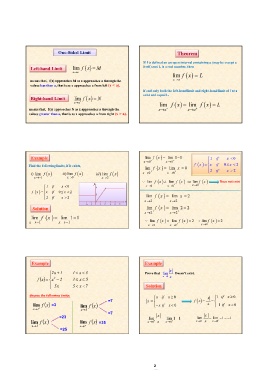
One-Sided Limit Theorem

Left-hand Limit lim f  x  M If f is defined on an open interval containing a (may be except a
itself) and L is a real number, then
xa
lim f  x  L
means that, f(x) approaches M as x approaches a through the
xa
values less than a, that is as x approaches a from left (x < a).

Right-hand Limit lim f  x  N if and only both the left-hand limit and right-hand limit of f at a
xa exist and equal L.

means that, f(x) approaches N as x approaches a through the lim f  x  lim f  x  L
xa xa
values greater than a, that is as x approaches a from right (x > a).

Example lim f  x   lim 1 1 1 if x 0
x 0 x 0 if 0x 2
f x    x if
Find the following limits, if it exists, lim f x   lim x  0  x 2
 2
i) lim f  x  ii) lim f  x  iii) lim f  x  x 0 x 0
x1 x0 x2
y
x 0  lim f x   lim f x   lim f x  Does not exist
0x 2 2 x 0 x 0 x 0
1 if
if x 2 1 lim f  x   lim x  2
f  x   x if
x 2 x 2
 2 x

2 1 12 34 5 lim f  x   lim 2  2

Solution x 2 x 2

lim f  x   lim 1  1  lim f  x   lim f  x   2  lim f x   2
x 1 x 1
x 2 x 2 x 2

Example Example
Prove that lim x Doesn’t exist.
2x  1 1 x 3
 3 x5 xx 0
f x   x2  2 5 x7
Solution
 5x

discuss the following limits: x if x0 x 1 if x0
 x if x0 x 1 if x0
lim f x =3 lim f x =7 x  f x  
=7
x1 x3

lim f x =23 lim f x =35 lim x  lim 1  1 lim x  lim 1  1
=25 x x 0 x
x5 x7  x 0 x 0 x 0

2