Page 48 - e-book PROGRAM LINEAR okeeee

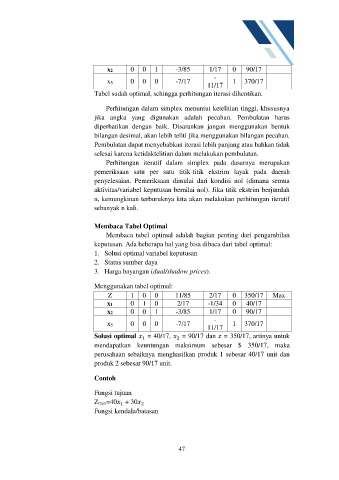
x2 0 0 1 -3/85 1/17 0 90/17
-
x5 0 0 0 -7/17 1 370/17
11/17
Tabel sudah optimal, sehingga perhitungan iterasi dihentikan.

Perhitungan dalam simplex menuntut ketelitian tinggi, khususnya
jika angka yang digunakan adalah pecahan. Pembulatan harus
diperhatikan dengan baik. Disarankan jangan menggunakan bentuk
bilangan desimal, akan lebih teliti jika menggunakan bilangan pecahan.
Pembulatan dapat menyebabkan iterasi lebih panjang atau bahkan tidak
selesai karena ketidaktelitian dalam melakukan pembulatan.
Perhitungan iteratif dalam simplex pada dasarnya merupakan
pemeriksaan satu per satu titik-titik ekstrim layak pada daerah
penyelesaian. Pemeriksaan dimulai dari kondisi nol (dimana semua
aktivitas/variabel keputusan bernilai nol). Jika titik ekstrim berjumlah
n, kemungkinan terburuknya kita akan melakukan perhitungan iteratif
sebanyak n kali.

Membaca Tabel Optimal
Membaca tabel optimal adalah bagian penting dari pengambilan
keputusan. Ada beberapa hal yang bisa dibaca dari tabel optimal:
1. Solusi optimal variabel keputusan
2. Status sumber daya
3. Harga bayangan (dual/shadow prices).

Menggunakan tabel optimal:
Z 1 0 0 11/85 2/17 0 350/17 Max
x1 0 1 0 2/17 -1/34 0 40/17
x2 0 0 1 -3/85 1/17 0 90/17
-
x5 0 0 0 -7/17 1 370/17
11/17
Solusi optimal = 40/17, = 90/17 dan = 350/17, artinya untuk
1
2
mendapatkan keuntungan maksimum sebesar $ 350/17, maka
perusahaan sebaiknya menghasilkan produk 1 sebesar 40/17 unit dan
produk 2 sebesar 90/17 unit.

Contoh

Fungsi tujuan
Zmax=40 + 30
1
2
Fungsi kendala/batasan

47