Page 5 - geometria

Geometría 5° Católica

10 RELACIONES MÉTRICAS EN TRIÁNGULOS

Semana RECTÁNGULOS

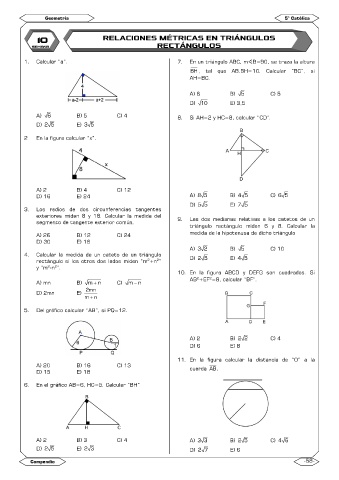
1. Calcular “a”. 7. En un triángulo ABC, mB=90, se traza la altura

BH , tal que AB.BH=10. Calcular “BC”, si
AH=BC.

A) 6 B) 5 C) 5
D) 10 E) 3,5

A) 6 B) 5 C) 4 8. Si AH=2 y HC=8, calcular “CD”.
D) 25 E) 35

2 En la figura calcular “x”.

A) 2 B) 4 C) 12
D) 16 E) 24 A) 85 B) 4 5 C) 65
D) 55 E) 75
3. Los radios de dos circunferencias tangentes
exteriores miden 8 y 18. Calcular la medida del
segmento de tangente exterior común. 9. Las dos medianas relativas a los catetos de un
triángulo rectángulo miden 6 y 8. Calcular la
A) 26 B) 12 C) 24 medida de la hipotenusa de dicho triángulo
D) 30 E) 16
A) 32 B) 5 C) 10
4. Calcular la medida de un cateto de un triángulo
2
rectángulo si los otros dos lados miden “m +n ” D) 25 E) 4 5
2
2
2
y “m -n ”.
10. En la figura ABCD y DEFG son cuadrados. Si
AB +EF =8, calcular “BF”.
2
2
A) mn B) m + n C) m n−
2mn
D) 2mn E)
m + n

5. Del gráfico calcular “AB”, si PQ=12.

A) 2 B) 22 C) 4
D) 6 E) 8

11. En la figura calcular la distancia de “O” a la
A) 20 B) 16 C) 13 cuerda AB .
D) 15 E) 18

6. En el gráfico AB=6, HC=5. Calcular “BH”

A) 2 B) 3 C) 4 A) 33 B) 25 C) 4 6
D) 25 E) 23 D) 2 7 E) 6

Compendio -58-