Page 26 - UNI M2 Geometria 5to sec
P. 26
Geometría 5° UNI
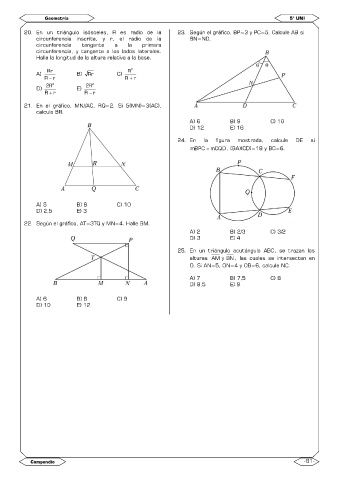
20. En un triángulo isósceles, R es radio de la 23. Según el gráfico, BP=3 y PC=5. Calcule AB si
circunferencia inscrita, y r, el radio de la BN=ND.
circunferencia tangente a la primera
circunferencia, y tangente a los lados laterales.
Halle la longitud de la altura relativa a la base.
Rr R 2
A) B) Rr C)
R − r R + r
2R 2 2R 2
D) E)
R + r R − r
21. En el gráfico, MN//AC, RQ=2. Si 5(MN)=3(AC),
calcule BR.
A) 6 B) 9 C) 10
D) 12 E) 16
24. En la figura mostrada, calcule DE si
mBPC = mCQD , (BA)(CD)=18 y BC=6.
A) 5 B) 8 C) 10
D) 2,5 E) 3
22. Según el gráfico, AT=3TQ y MN=4. Halle BM.
A) 2 B) 2/3 C) 3/2
D) 3 E) 4
25. En un triángulo acutángulo ABC, se trazan las
alturas AM y BN , las cuales se intersectan en
O. Si AN=5, ON=4 y OB=6, calcule NC.
A) 7 B) 7,5 C) 8
D) 8,5 E) 9
A) 6 B) 8 C) 9
D) 10 E) 12
Compendio -61-