Page 27 - KI - geometria 2 sec

Geometría 2° Secundaria

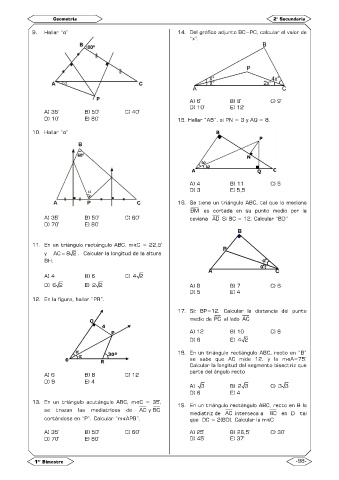
9. Hallar “α” 14. Del gráfico adjunto BC=PC, calcular el valor de
“x”.

A) 6̊ B) 8̊ C) 9̊
D) 10̊ E) 12̊
A) 35̊ B) 50̊ C) 40̊
D) 10̊ E) 80̊ 15. Hallar “AB”, si PN = 3 y AQ = 8.

10. Hallar “α”

A) 4 B) 11 C) 5
D) 3 E) 5,5

16. Se tiene un triángulo ABC, tal que la mediana
BM es cortada en su punto medio por la
A) 35̊ B) 50̊ C) 60̊ ceviana AD Si BC = 12. Calcular “BD”
D) 70̊ E) 80̊

11. En un triángulo rectángulo ABC, m∢C = 22,5̊
y AC  8 2 . Calcular la longitud de la altura
BH.

A) 4 B) 6 C) 4 2

D) 6 2 E) 2 2 A) 8 B) 7 C) 6
D) 5 E) 4
12. En la figura, hallar “PR”.

17. Si: BP=12. Calcular la distancia del punto
medio de PC al lado AC

A) 12 B) 10 C) 8
D) 6 E) 4 2

18. En un triángulo rectángulo ABC, recto en “B”
se sabe que AC mide 12, y la m∢A=75̊.

Calcular la longitud del segmento bisectriz que
parte del ángulo recto
A) 6 B) 8 C) 12
D) 9 E) 4
A) 3 B) 2 3 C) 3 3
D) 6 E) 4
13. En un triángulo acutángulo ABC, m∢C = 35̊, 19. En un triángulo rectángulo ABC, recto en B la
se trazan las mediatrices de AC y BC
mediatriz de AC interseca a BC en D tal
cortándose en “P”. Calcular “m∢APB”. que DC = 2(BD). Calcular la m∢C

A) 35̊ B) 50̊ C) 60̊ A) 25̊ B) 26,5̊ C) 30̊
D) 70̊ E) 80̊ D) 45̊ E) 37̊

1 Bimestre -98-
er