Page 16 - SM GEOMETRIA 5

Geometría 5° San Marcos

30
Semana

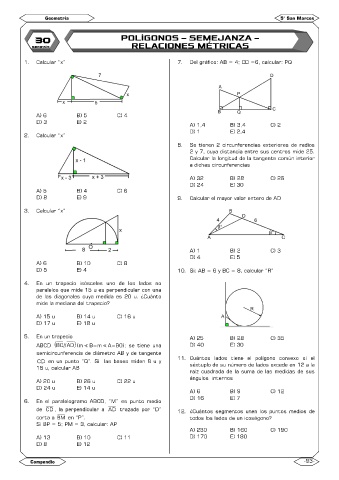
1. Calcular “x” 7. Del gráfico: AB = 4; CD =6, calcular: PQ

A) 6 B) 5 C) 4
D) 3 E) 2 A) 1,4 B) 3,4 C) 2
D) 1 E) 2,4
2. Calcular “x”

8. Se tienen 2 circunferencias exteriores de radios
2 y 7, cuya distancia entre sus centros mide 25.
Calcular la longitud de la tangente común interior
a dichas circunferencias

A) 32 B) 28 C) 26
D) 24 E) 30
A) 5 B) 4 C) 6
D) 8 E) 9 9. Calcular el mayor valor entero de AD

3. Calcular “x”

A) 1 B) 2 C) 3
D) 4 E) 5
A) 6 B) 10 C) 8
D) 5 E) 4 10. Si: AB = 6 y BC = 8, calcular “R”

4. En un trapecio isósceles uno de los lados no
paralelos que mide 15 u es perpendicular con una
de las diagonales cuya medida es 20 u. ¿Cuánto
mide la mediana del trapecio?

A) 15 u B) 14 u C) 16 u
D) 17 u E) 18 u

5. En un trapecio A) 25 B) 28 C) 35
)
ABCD (BC//AD (m B=m A=90); se tiene una D) 40 E) 30
semicircunferencia de diámetro AB y de tangente
CD en un punto “Q”. Si las bases miden 8 u y 11. Cuántos lados tiene el polígono convexo si el
18 u, calcular AB séxtuplo de su número de lados excede en 12 a la
raíz cuadrada de la suma de las medidas de sus
ángulos internos
A) 20 u B) 26 u C) 22 u
D) 24 u E) 14 u
A) 6 B) 9 C) 12
E) 7
D) 16
6. En el paralelogramo ABCD, “M” es punto medio
de CD , la perpendicular a AD trazada por “D” 12. ¿Cuántos segmentos unen los puntos medios de
corta a BM en “P”. todos los lados de un icoságono?
Si BP = 5; PM = 3, calcular: AP
A) 230 B) 160 C) 190
A) 13 B) 10 C) 11 D) 170 E) 180
D) 8 E) 12

Compendio -93-