Page 89 - KM Matematika-BS-KLS-VIII-Baru_Neat

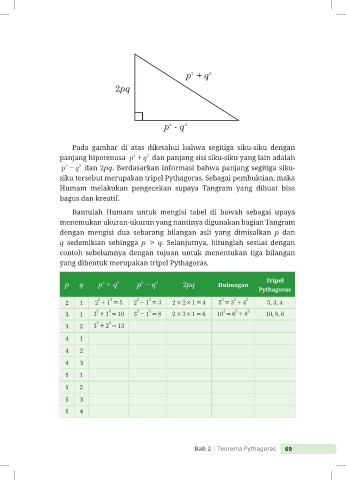
p + q 2
2
2pq

p - q 2
2

Pada gambar di atas diketahui bahwa segitiga siku-siku dengan
2
panjang hipotenusa p + q dan panjang sisi siku-siku yang lain adalah
2
p - q 2 dan 2pq. Berdasarkan informasi bahwa panjang segitiga siku-
2
siku tersebut merupakan tripel Pythagoras. Sebagai pembuktian, maka
Humam melakukan pengecekan supaya Tangram yang dibuat bisa
bagus dan kreatif.

Bantulah Humam untuk mengisi tabel di bawah sebagai upaya
menemukan ukuran-ukuran yang nantinya digunakan bagian Tangram
dengan mengisi dua sebarang bilangan asli yang dimisalkan p dan
q sedemikian sehingga p > q. Selanjutnya, hitunglah sesuai dengan
contoh sebelumnya dengan tujuan untuk menentukan tiga bilangan
yang dibentuk merupakan tripel Pythagoras.

Tripel
2
2
2
2
p q p + q p - q 2pq Hubungan
Pythagoras
2 2 2 2 2 2 2
2 1 2 + 1 = 5 2 - 1 = 3 2 × 2× 1 = 4 5 = 3 + 4 5, 3, 4
2 2 2 2 2 2 2
3 1 3 + 1 = 10 3 - 1 = 8 2 × 3× 1 = 6 10 = 6 + 8 10, 8, 6
2 2
3 2 3 + 2 = 13
4 1
4 2
4 3
5 1

5 2
5 3
5 4

Bab 2 | Teorema Pythagoras 69