Page 21 - u4

P2: OSO/OVY
QC: OSO/OVY
T1: OSO
P1: OSO/OVY
UAE_Math_Grade_12_Vol_1_SE_718383_ch3
July 4, 2016
13:38
GO01962-Smith-v1.cls
Solution From Definition 1.1, the linear approximation is defined as
y ′ ′
L(x) = f(x ) + f (x )(x − x ). Here, x = ∕3,f(x) = cos x and f (x) = − sin x. So,
0
0
0
0
we have
√

( ) ( )( ) 1 3 ( )
L(x) = cos − sin x − = − x − .
3 3 3 2 2 3
π
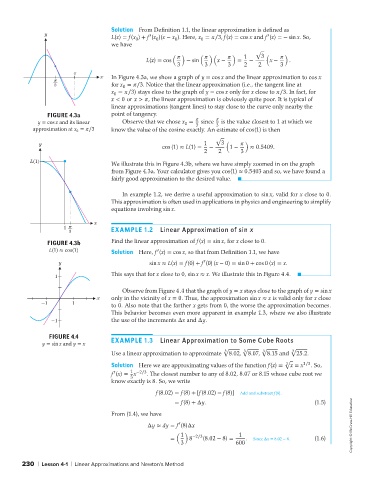
x In Figure 4.3a, we show a graph of y = cos x and the linear approximation to cos x
π
3 for x = ∕3. Notice that the linear approximation (i.e., the tangent line at
0
x = ∕3) stays close to the graph of y = cos x only for x close to ∕3. In fact, for
0
x < 0 or x > , the linear approximation is obviously quite poor. It is typical of
linear approximations (tangent lines) to stay close to the curve only nearby the
FIGURE 4.3a point of tangency.
y = cos x and its linear Observe that we chose x = 3 since 3 is the value closest to 1 at which we
0
approximation at x = ∕3 know the value of the cosine exactly. An estimate of cos(1) is then
0
√
y cos (1) ≈ L(1) = 1 − 3 ( 1 − ) ≈ 0.5409.
2 2 3
L(1) We illustrate this in Figure 4.3b, where we have simply zoomed in on the graph
from Figure 4.3a. Your calculator gives you cos(1) ≈ 0.5403 and so, we have found a
fairly good approximation to the desired value.
In example 1.2, we derive a useful approximation to sin x, valid for x close to 0.
This approximation is often used in applications in physics and engineering to simplify
equations involving sin x.
x
1 π EXAMPLE 1.2 Linear Approximation of sin x
3
FIGURE 4.3b Find the linear approximation of f(x) = sin x, for x close to 0.
L(1) ≈ cos(1) Solution Here, f (x) = cos x, so that from Definition 1.1, we have
′
′
y sin x ≈ L(x) = f(0) + f (0) (x − 0) = sin 0 + cos 0(x) = x.
This says that for x close to 0, sin x ≈ x. We illustrate this in Figure 4.4.
1
Observe from Figure 4.4 that the graph of y = x stays close to the graph of y = sin x
x only in the vicinity of x = 0. Thus, the approximation sin x ≈ x is valid only for x close
-1 1 to 0. Also note that the farther x gets from 0, the worse the approximation becomes.
This behavior becomes even more apparent in example 1.3, where we also illustrate
-1 the use of the increments Δx and Δy.

FIGURE 4.4
y = sin x and y = x EXAMPLE 1.3 Linear Approximation to Some Cube Roots
√ √ √ √
3
3
3
3
Use a linear approximation to approximate 8.02, 8.07, 8.15 and 25.2.
3
Solution Here we are approximating values of the function f(x) = √ x = x 1∕3 . So,
′
1 −2∕3
f (x) = x . The closest number to any of 8.02, 8.07 or 8.15 whose cube root we
3
know exactly is 8. So, we write
f(8.02) = f(8) + [f(8.02) − f(8)] Add and substract f(8).
= f(8) +Δy. (1.5)
From (1.4), we have
′
Δy ≈ dy = f (8)Δx Copyright © McGraw-Hill Education
1
( ) 1
= 8 −2∕3 (8.02 − 8) = . Since Δx = 8.02 − 8. (1.6)
3 600
230 | Lesson 4-1 | Linear Approximations and Newton’s Method