Page 23 - u4

T1: OSO
P2: OSO/OVY
P1: OSO/OVY
GO01962-Smith-v1.cls
UAE_Math_Grade_12_Vol_1_SE_718383_ch3
13:38
July 4, 2016
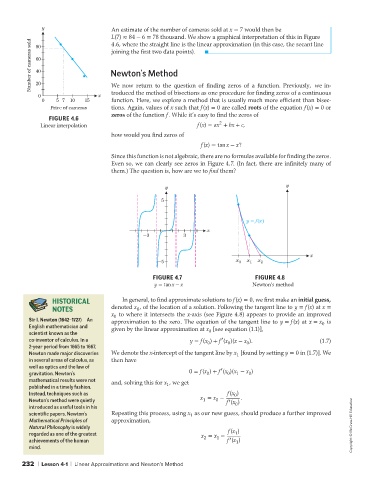
y QC: OSO/OVY An estimate of the number of cameras sold at x = 7 would then be
L(7) ≈ 84 − 6 = 78 thousand. We show a graphical interpretation of this in Figure
Number of cameras sold 60 Newton’s Method
4.6, where the straight line is the linear approximation (in this case, the secant line
80
joining the first two data points).
40
20
troduced the method of bisections as one procedure for finding zeros of a continuous
0 x We now return to the question of finding zeros of a function. Previously, we in-
0 57 10 15 function. Here, we explore a method that is usually much more efficient than bisec-
Price of cameras tions. Again, values of x such that f(x) = 0 are called roots of the equation f(x) = 0 or
zeros of the function f. While it’s easy to find the zeros of
FIGURE 4.6
2
Linear interpolation f(x) = ax + bx + c,
how would you find zeros of
f(x) = tan x − x?
Since this function is not algebraic, there are no formulas available for finding the zeros.
Even so, we can clearly see zeros in Figure 4.7. (In fact, there are infinitely many of
them.) The question is, how are we to find them?

y y
5

y = f(x)
x
-3 3

x
-5 x 0 x 1 x 2

FIGURE 4.7 FIGURE 4.8
y = tan x − x Newton’s method

HISTORICAL In general, to find approximate solutions to f(x) = 0, we first make an initial guess,
NOTES denoted x , of the location of a solution. Following the tangent line to y = f(x) at x =
0
x to where it intersects the x-axis (see Figure 4.8) appears to provide an improved
0
Sir I. Newton (1642–1727) An approximation to the zero. The equation of the tangent line to y = f(x) at x = x is
English mathematician and given by the linear approximation at x [see equation (1.1)], 0
scientist known as the 0
′
co-inventor of calculus. In a y = f(x ) + f (x )(x − x ). (1.7)
2-year period from 1665 to 1667, 0 0 0
Newton made major discoveries We denote the x-intercept of the tangent line by x [found by setting y = 0 in (1.7)]. We
1
in several areas of calculus, as then have
well as optics and the law of ′
gravitation. Newton’s 0 = f(x ) + f (x )(x − x )
0
0
0
1
mathematical results were not and, solving this for x ,weget
published in a timely fashion. 1
Instead, techniques such as f(x )
0
0
1
Newton’s method were quietly x = x − f (x ) .
′
introduced as useful tools in his 0
scientific papers. Newton’s Repeating this process, using x as our new guess, should produce a further improved
1
Mathematical Principles of approximation,
Natural Philosophy is widely f(x ) Copyright © McGraw-Hill Education
regarded as one of the greatest x = x − 1
′
achievements of the human 2 1 f (x )
1
mind.
232 | Lesson 4-1 | Linear Approximations and Newton’s Method