Page 26 - u4
P. 26
P2: OSO/OVY
P1: OSO/OVY
UAE_Math_Grade_12_Vol_1_SE_718383_ch3
GO01962-Smith-v1.cls
n x n QC: OSO/OVY T1: OSO July 4, 2016 13:38
1 −9.5 EXAMPLE 1.8 Unusually Slow Convergence for Newton’s Method
2 −65.9 Use Newton’s method with (a) x =−2, (b) x =−1 and (c) x = 0 to try to locate
0
0
0
3 −2302 the zero of f(x) = (x − 1) 2 .
2
4 −2,654,301 x + 1
5 −3.5 × 10 12 Solution Of course, there’s no mystery here: f has only one zero, located at x = 1.
6 −6.2 × 10 24 However, watch what happens when we use Newton’s method with the specified
guesses.
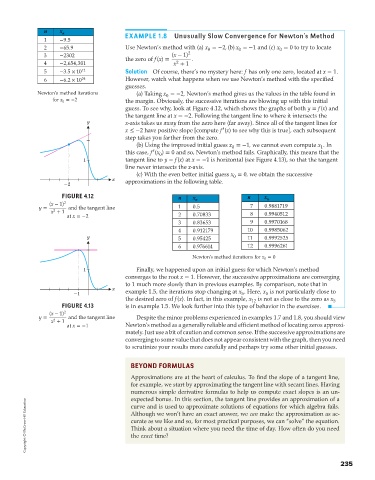
Newton’s method iterations (a) Taking x =−2, Newton’s method gives us the values in the table found in
0
for x =−2 the margin. Obviously, the successive iterations are blowing up with this initial
0
guess. To see why, look at Figure 4.12, which shows the graphs of both y = f(x) and
the tangent line at x =−2. Following the tangent line to where it intersects the
y x-axis takes us away from the zero here (far away). Since all of the tangent lines for
′
x ≤ −2 have positive slope [compute f (x) to see why this is true], each subsequent
step takes you farther from the zero.
(b) Using the improved initial guess x =−1, we cannot even compute x . In
0
1
′
this case, f (x ) = 0 and so, Newton’s method fails. Graphically, this means that the
0
1 tangent line to y = f(x) at x =−1 is horizontal (see Figure 4.13), so that the tangent
line never intersects the x-axis.
(c) With the even better initial guess x = 0, we obtain the successive
x approximations in the following table. 0
-2
FIGURE 4.12 n x n x n
(x − 1) 2 n
y = and the tangent line 1 0.5 7 0.9881719
x + 1 8 0.9940512
2
at x =−2 2 0.70833
3 0.83653 9 0.9970168
4 0.912179 10 0.9985062
y 5 0.95425 11 0.9992525
6 0.976614 12 0.9996261
Newton’s method iterations for x = 0
0
1 Finally, we happened upon an initial guess for which Newton’s method
converges to the root x = 1. However, the successive approximations are converging
to 1 much more slowly than in previous examples. By comparison, note that in
x
5
5
-1 example 1.5, the iterations stop changing at x . Here, x is not particularly close to
the desired zero of f(x). In fact, in this example, x 12 is not as close to the zero as x 5
FIGURE 4.13 is in example 1.5. We look further into this type of behavior in the exercises.
(x − 1) 2
y = and the tangent line Despite the minor problems experienced in examples 1.7 and 1.8, you should view
x + 1
2
at x =−1 Newton’s method as a generally reliable and efficient method of locating zeros approxi-
mately. Just use a bit of caution and common sense. If the successive approximations are
converging to some value that does not appear consistent with the graph, then you need
to scrutinize your results more carefully and perhaps try some other initial guesses.
BEYOND FORMULAS
Approximations are at the heart of calculus. To find the slope of a tangent line,
for example, we start by approximating the tangent line with secant lines. Having
numerous simple derivative formulas to help us compute exact slopes is an un-
expected bonus. In this section, the tangent line provides an approximation of a
Copyright © McGraw-Hill Education Although we won’t have an exact answer, we can make the approximation as ac-
curve and is used to approximate solutions of equations for which algebra fails.
curate as we like and so, for most practical purposes, we can “solve” the equation.
Think about a situation where you need the time of day. How often do you need
the exact time?
235