Page 9 - TOPIK 4 - a. GELOMBANG DAN OPTIK

Substitusi = 2 dan = 2 / ke persamaan (15), kita memperoleh

( , ) = sin( − ) (17)

Sebagai tambahan, menggunakan hubungan = dan 2 = , kita
memperoleh

= (18)

Walaupun kita menggunakan fungsi sinus pada persamaan
sebelumnya, kita dapat juga menggunakan fungsi kosinus seperi

berikut

( , ) = cos( − ) (19)

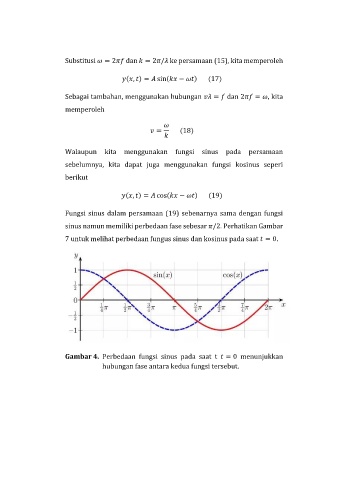
Fungsi sinus dalam persamaan (19) sebenarnya sama dengan fungsi
sinus namun memiliki perbedaan fase sebesar /2. Perhatikan Gambar
7 untuk melihat perbedaan fungus sinus dan kosinus pada saat = 0.

Gambar 4. Perbedaan fungsi sinus pada saat t = 0 menunjukkan
hubungan fase antara kedua fungsi tersebut.