Page 10 - HS 6 spreidingsdiagrammen correlatie regressie

Statistiek in de tweede graad

6.3 De correlatiecoëfficiënt: numeriek onderzoek van de correlatie

Uit de vorige paragraaf blijkt dat het mogelijk is om met een spreidingsdiagram de richting van de
samenhang (positief/negatief) in te schatten. Het is heel wat moeilijker om de sterkte van deze
samenhang in te schatten. Vandaar de noodzaak om de samenhang iets nauwkeuriger ook met een
getal (numeriek) weer te geven.
6.3.1 Zwaartepunt van een spreidingsdiagram

Om te onderzoeken of er enig verband (correlatie) bestaat tussen de lengte van een moeder en die van
haar dochter zijn de lengtes van 12 moeders en die van hun oudste dochter gemeten op het moment
dat die dochters volwassen werden. De gegevens staan in de volgende tabel:

Lengte moeder in cm 168 163 175 165 175 160 180 170 176 173 178 185

Lengte dochter in cm 174 170 170 168 178 170 173 177 180 176 177 181
tabel.
Wij berekenen ook het gemiddelde van de lengte van de moeders en het gemiddelde van de lengte van
de dochters.
̅
̅
Gemiddelde lengte moeders: = 172,3 en gemiddelde lengte dochter: = 174,5

Uiteraard zullen de punten van het spreidingsdiagram gelegen zijn rond het punt
̅
̅
( , ) = (172,3; 174,5)

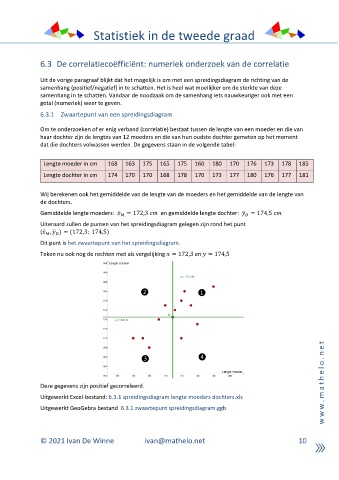
Dit punt is het zwaartepunt van het spreidingsdiagram.
Teken nu ook nog de rechten met als vergelijking = 172,3 en = 174,5

❷ ❶

t
e
n
❸ ❹ .
o
l
e
h
Deze gegevens zijn positief gecorreleerd. t
a
Uitgewerkt Excel-bestand: 6.3.1 spreidingsdiagram lengte moeders dochters.xls m
.
Uitgewerkt GeoGebra bestand 6.3.1 zwaartepunt spreidingsdiagram.ggb w
w

w

© 2021 Ivan De Winne ivan@mathelo.net 10