Page 11 - HS 6 spreidingsdiagrammen correlatie regressie
P. 11
Statistiek in de tweede graad
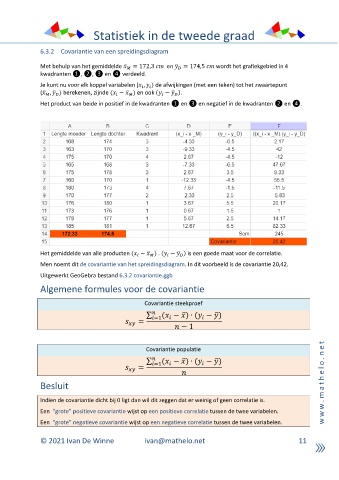
6.3.2 Covariantie van een spreidingsdiagram
̅
̅
Met behulp van het gemiddelde = 172,3 en = 174,5 wordt het grafiekgebied in 4
kwadranten ❶, ❷, ❸ en ❹ verdeeld.
Je kunt nu voor elk koppel variabelen ( , ) de afwijkingen (met een teken) tot het zwaartepunt
̅
̅
̅
̅
( , ) berekenen, zijnde ( − ) en ook ( − ).
Het product van beide in positief in de kwadranten ❶ en ❸ en negatief in de kwadranten ❷ en ❹.
̅
Het gemiddelde van alle producten ( − ) . ( − ) is een goede maat voor de correlatie.
̅
Men noemt dit de covariantie van het spreidingsdiagram. In dit voorbeeld is de covariantie 20,42.
Uitgewerkt GeoGebra bestand 6.3.2 covariantie.ggb
Algemene formules voor de covariantie
Covariantie steekproef
̅
∑ ( − ) ∙ ( − )
̅
=1
=
− 1
t
Covariantie populatie e
n
∑ ( − ) ∙ ( − ) . o
̅
̅
=1
= l
e
h
Besluit t a
m
Indien de covariantie dicht bij 0 ligt dan wil dit zeggen dat er weinig of geen correlatie is. .
w
Een “grote” positieve covariantie wijst op een positieve correlatie tussen de twee variabelen.
w
Een “grote” negatieve covariantie wijst op een negatieve correlatie tussen de twee variabelen. w
© 2021 Ivan De Winne ivan@mathelo.net 11