Page 2 - HS 4 Rijen in de 3de graad
P. 2
GeoGebra in de derde graad
2. n is oneven
Indien n oneven is dan werkt de vorige werkwijze niet.
Beschouw bijvoorbeeld de som van de eerste 7 natuurlijke getallen: 1 + 2 + 3 + 4 + 5 + 6 +7
De som is in dit geval (1 + 7) + (2 + 6) + (3 + 5) + 4 =20
Algemeen geldt er in dit geval:
−1 +1
keer ( + 1) Hierbij moet nog het middelste getal opgeteld worden.
2 2
Het eindresultaat is dan:
−1 +1 ( −1)+1 ∙( +1)
= 2 ∙ ( + 1) + 2 = 2 ∙ ( + 1) = 2 ( ∈ )
0
3. Eleganter bewijs
Zet de optelling van de eerste n natuurlijke getallen twee keer in tegengestelde volgorde onder elkaar
en tel op.
= 1 + 2 + 3+. . . + − 1 +
= + − 1+ . .. +3 + 2 + 1
Dus:
2 = ∙ ( + 1)
Waaruit volgt:
∙( +1)
= 2 ( ∈ )
0
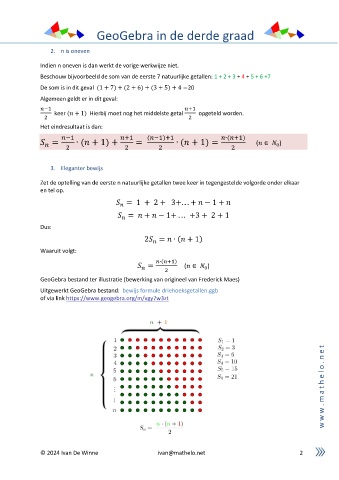
GeoGebra bestand ter illustratie (bewerking van origineel van Frederick Maes)
Uitgewerkt GeoGebra bestand: bewijs formule driehoeksgetallen.ggb
of via link https://www.geogebra.org/m/vgy7w3zt
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© 2024 Ivan De Winne ivan@mathelo.net 2