Page 25 - HS 4 Rijen in de 3de graad

GeoGebra in de derde graad

4.12 Methode van Heron
De methode van Heron is een benadering voor de berekening van de vierkantswortel uit een (positief)
reëel getal met een recursieformule.

Bron Wikipedia https://nl.wikipedia.org/wiki/Methode_van_Heron
Deze methode werd rond 100 van onze jaartelling beschreven door Heron van Alexandrië in zijn boek
Metrica.
Voorbeeld: benadering van √3

Beschouw de rij met recursief voorschrift:
 u = 1
1

 u = 1 .(u + 3 )
 n+ 1 n
 2 u n

Blijkbaar convergeert deze rij van getallen naar 3
GeoGebra is een uitstekend hulpmiddel om dit te visualiseren.

 Maak een schuifknop n met waarden tussen 1 en 20 met stapgrootte 1

 Typ in het algebravenster de waarde voor de eerste term u_1 = 1

 Typ in het algebravenster het functievoorschrift f(x) =1 / 2*(x + 3 / x)
en maak de grafiek onzichtbaar.

 Maak vervolgens een lijst van getallen voor opeenvolgende waarden van n.
L1=IteratieLijst(f, u_1, n – 1) Dit zijn de eerste n waarden van de rij.

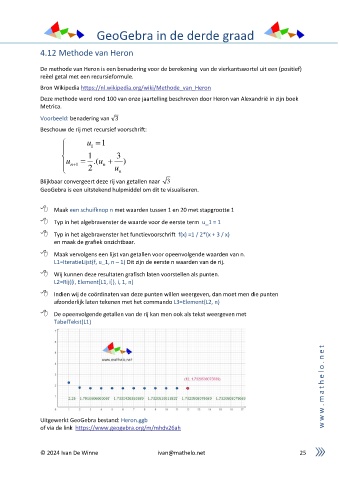
 Wij kunnen deze resultaten grafisch laten voorstellen als punten.
L2=Rij((i, Element[L1, i]), i, 1, n)

 Indien wij de coördinaten van deze punten willen weergeven, dan moet men die punten
afzonderlijk laten tekenen met het commando L3=Element(L2, n)
 De opeenvolgende getallen van de rij kan men ook als tekst weergeven met
TabelTekst(L1)

t
e
n
.
o
l
e
h
t
a
m
.
w

Uitgewerkt GeoGebra bestand: Heron.ggb w
of via de link https://www.geogebra.org/m/mhdv26ah w

© 2024 Ivan De Winne ivan@mathelo.net 25