Page 20 - HS 4 Rijen in de 3de graad
P. 20
GeoGebra in de derde graad
4.10 Webgrafieken voor meetkundige rijen
Doe de nodige aanpassingen in het vorige bestand en onderzoek met webgrafieken de convergentie van
meetkundige rijen.
Beschouw een meetkundige rij met reden ≠ 1
Het recursief voorschrift van een meetkundige rij is +1 = ∙ en is gegeven ( ∈ ).
0
1
We tekenen in een aantal gevallen de webgrafiek van deze meetkundige rij en onderzoeken of deze
meetkundige rij convergent (naderend naar grenswaarde zijnde een reëel getal) of divergent (niet
naderend naar een grenswaarde.
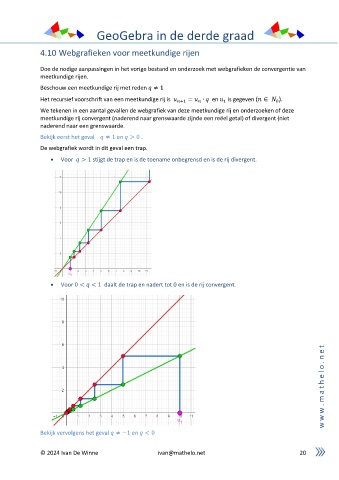
Bekijk eerst het geval ≠ 1 en > 0 .
De webgrafiek wordt in dit geval een trap.
• Voor > 1 stijgt de trap en is de toename onbegrensd en is de rij divergent.
• Voor 0 < < 1 daalt de trap en nadert tot 0 en is de rij convergent.
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
Bekijk vervolgens het geval ≠ −1 en < 0
© 2024 Ivan De Winne ivan@mathelo.net 20