Page 19 - HS 4 Rijen in de 3de graad

GeoGebra in de derde graad

4.9 Webgrafiek

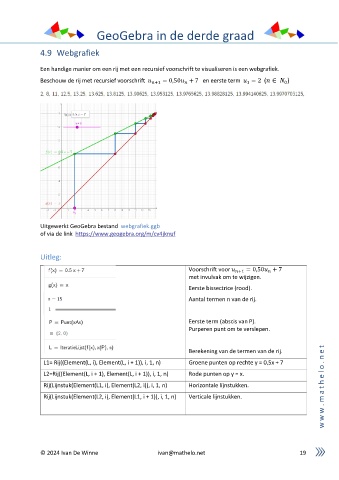
Een handige manier om een rij met een recursief voorschrift te visualiseren is een webgrafiek.

Beschouw de rij met recursief voorschrift +1 = 0,50 + 7 en eerste term = 2 ( ∈ )
0
1

Uitgewerkt GeoGebra bestand webgrafiek.ggb
of via de link https://www.geogebra.org/m/cv4jknuf

Uitleg:
Voorschrift voor +1 = 0,50 + 7

met invulvak om te wijzigen.
Eerste bissectrice (rood).

Aantal termen n van de rij.

Eerste term (abscis van P).
Purperen punt om te verslepen.

t
Berekening van de termen van de rij. e
n
L1= Rij((Element(L, i), Element(L, i + 1)), i, 1, n) Groene punten op rechte y = 0,5x + 7 .
o
L2=Rij((Element(L, i + 1), Element(L, i + 1)), i, 1, n) Rode punten op y = x. l
e
h
Rij(Lijnstuk(Element(L1, i), Element(L2, i)), i, 1, n) Horizontale lijnstukken.
t
a
Rij(Lijnstuk(Element(L2, i), Element(L1, i + 1)), i, 1, n) Verticale lijnstukken.
m
.
w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 19