Page 13 - HS 6 Photomath

A.I. voor wiskunde

6.5.2 Bespreking van een veeltermfunctie met graad groter dan 2

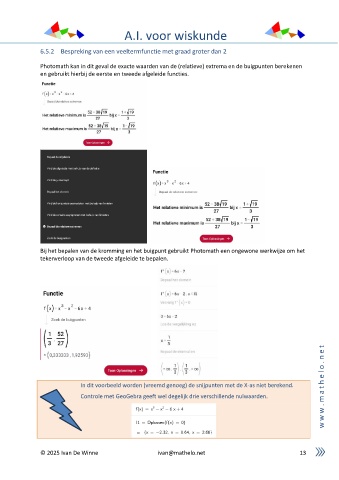
Photomath kan in dit geval de exacte waarden van de (relatieve) extrema en de buigpunten berekenen
en gebruikt hierbij de eerste en tweede afgeleide functies.

Bij het bepalen van de kromming en het buigpunt gebruikt Photomath een ongewone werkwijze om het
tekenverloop van de tweede afgeleide te bepalen.

t
e
n
.
o
l
e
h
In dit voorbeeld worden (vreemd genoeg) de snijpunten met de X-as niet berekend.
t
a
Controle met GeoGebra geeft wel degelijk drie verschillende nulwaarden.
m
.
w
w
w

© 2025 Ivan De Winne ivan@mathelo.net 13