Page 34 - Geogebra 6 van A tot Z
P. 34
GeoGebra 6 van A tot Z
2.4 De maantjes van Hippocrates (met bewijs)
Maak een tekening ter illustratie van de volgende merkwaardige eigenschap.
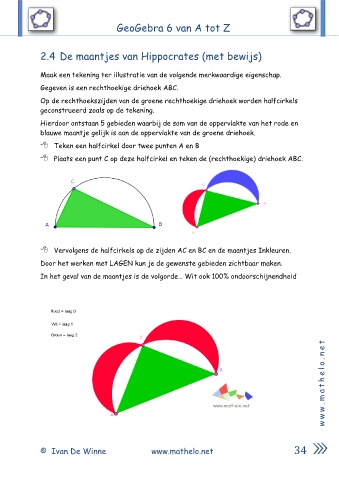
Gegeven is een rechthoekige driehoek ABC.
Op de rechthoekszijden van de groene rechthoekige driehoek worden halfcirkels
geconstrueerd zoals op de tekening.
Hierdoor ontstaan 5 gebieden waarbij de som van de oppervlakte van het rode en
blauwe maantje gelijk is aan de oppervlakte van de groene driehoek.
Teken een halfcirkel door twee punten A en B
Plaats een punt C op deze halfcirkel en teken de (rechthoekige) driehoek ABC.
Vervolgens de halfcirkels op de zijden AC en BC en de maantjes Inkleuren.
Door het werken met LAGEN kun je de gewenste gebieden zichtbaar maken.
In het geval van de maantjes is de volgorde… Wit ook 100% ondoorschijnendheid
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 34