Page 35 - Geogebra 6 van A tot Z
P. 35
GeoGebra 6 van A tot Z
2.4.1 Berekening van de oppervlakte van de maantjes
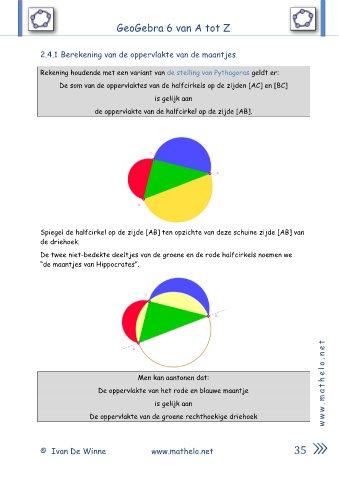
Rekening houdende met een variant van de stelling van Pythagoras geldt er:
De som van de oppervlaktes van de halfcirkels op de zijden [AC] en [BC]
is gelijk aan
de oppervlakte van de halfcirkel op de zijde [AB].
Spiegel de halfcirkel op de zijde [AB] ten opzichte van deze schuine zijde [AB] van
de driehoek.
De twee niet-bedekte deeltjes van de groene en de rode halfcirkels noemen we
“de maantjes van Hippocrates”.
t
e
n
.
o l
Men kan aantonen dat: e h
De oppervlakte van het rode en blauwe maantje t a
m
is gelijk aan .
w
De oppervlakte van de groene rechthoekige driehoek w
w
© Ivan De Winne www.mathelo.net 35