Page 7 - HS 7 Inleiding goniometrische functies

P. 7

GeoGebra in de derde graad

7.4 De goniometrische functies

7.4.1 De sinusfunctie

Je kan nu met de goniometrische getallen ook de overeenkomstige goniometrische functies definiëren;
f(x) = sin(x) waarbij x wordt gemeten in radialen.
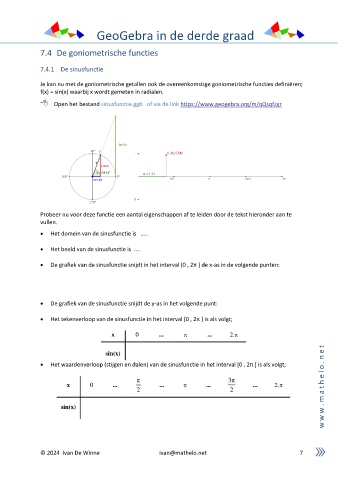
 Open het bestand sinusfunctie.ggb of via de link https://www.geogebra.org/m/qQsqfzgr

Probeer nu voor deze functie een aantal eigenschappen af te leiden door de tekst hieronder aan te
vullen.

• Het domein van de sinusfunctie is …..

• Het beeld van de sinusfunctie is ….

• De grafiek van de sinusfunctie snijdt in het interval [0 , 2π ] de x-as in de volgende punten:

• De grafiek van de sinusfunctie snijdt de y-as in het volgende punt:

• Het tekenverloop van de sinusfunctie in het interval [0 , 2π ] is als volgt;

x 0 ...  ... 2.

t
sin(x) e
n
• Het waardenverloop (stijgen en dalen) van de sinusfunctie in het interval [0 , 2π ] is als volgt; . o
l
π 3π e
x 0 ... ...  ... ... 2. h
2 2 t
a
m
sin(x) .
w
w

2 3 4 5 6 7 8 9 10 11 12