Page 20 - HS 3 Regressie en correlatie
P. 20
Combinatieleer, kansrekening en verklarende statistiek
3.5 Methode van de kleinste kwadraten
3.5.1 Visualisatie van de methode
Het opstellen van de regressielijn (bij lineaire regressie) kan opgevat worden als het bepalen van de
“best passende rechte” bij het spreidingsdiagram van de gegeven data.
De beroemde wiskundige Gauss bedacht hiervoor in de negentiende eeuw de methode van de kleinste
kwadraten.
Stel dat de vergelijking van de regressielijn (van y op x) van de vorm y = a.x + b is.
De methode van Gauss betekent dan dat de som van de kwadraten van de verticale afwijkingen van
de gegeven meetpunten (van het spreidingsdiagram) tot deze regressielijn minimaal moet zijn.
Gegeven is het spreidingsdiagram van een dataset uit 3.4.1
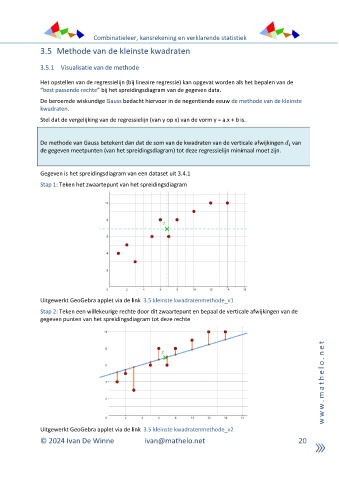
Stap 1: Teken het zwaartepunt van het spreidingsdiagram
Uitgewerkt GeoGebra applet via de link 3.5 kleinste kwadratenmethode_v1
Stap 2: Teken een willekeurige rechte door dit zwaartepunt en bepaal de verticale afwijkingen van de
gegeven punten van het spreidingsdiagram tot deze rechte
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
Uitgewerkt GeoGebra applet via de link 3.5 kleinste kwadratenmethode_v2
© 2024 Ivan De Winne ivan@mathelo.net 20