Page 3 - 08_Dontsov

мов отстрела ложных тепловых целей (ЛТЦ). Поэтому актуальна задача оценки защищенно-
сти летательных аппаратов, оснащенных устройствами отстрела ЛТЦ, от управляемого ору-
жия с ГСН матричного типа и разработки специального математического обеспечения.
Цель работы – разработка математической модели процесса поражения летательного
аппарата, оснащенного устройствами отстрела ложных тепловых целей, от управляемого
оружия с оптическими головками самонаведения матричного типа.

Alexander A. Dontsov, Yuri L. Koziratsky… Mathematical Model of the Process of Destruc-tion of the Aircraft Guidance…
Описание математической модели
Описание математической модели
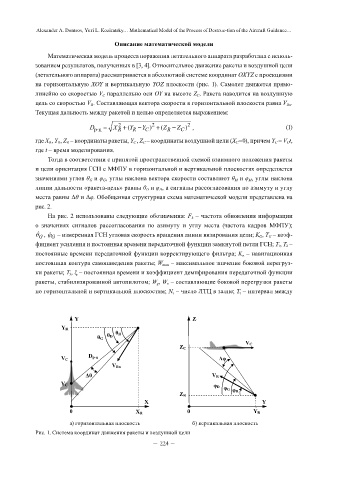
Математическая модель процесса поражения летательного аппарата разработана с ис-
Математическая модель процесса поражения летательного аппарата разработана с исполь-
пользованием результатов, полученных в [3, 4]. Относительное движение ракеты и воздуш-
зованием результатов, полученных в [3, 4]. Относительное движение ракеты и воздушной цели
ной цели (летательного аппарата) рассматривается в абсолютной системе координат OXYZ с
(летательного аппарата) рассматривается в абсолютной системе координат OXYZ с проекциями
мов отстрела ложных тепловых целей (ЛТЦ). Поэтому актуальна задача оценки защищенно-
проекциями на горизонтальную XOY и вертикальную YOZ плоскости (рис. 1). Самолет дви-
на горизонтальную XOY и вертикальную YOZ плоскости (рис. 1). Самолет движется прямо-
жется прямолинейно со скоростью V С параллельно оси OY на высоте Z С. Ракета наводится на
сти летательных аппаратов, оснащенных устройствами отстрела ЛТЦ, от управляемого ору-
линейно со скоростью V С параллельно оси OY на высоте Z С . Ракета наводится на воздушную
воздушную цель со скоростью V R. Составляющая вектора скорости в горизонтальной плос-
цель со скоростью V R . Составляющая вектора скорости в горизонтальной плоскости равна V Rп .
жия с ГСН матричного типа и разработки специального математического обеспечения.
Текущая дальность между ракетой и целью определяется выражением: и целью определяется выражением:
кости равна V Rп. Текущая дальность между ракетой
Цель работы – разработка математической модели процесса поражения летательного
2

D
р-ц устройствами отстрела ложных тепловых целей, от управляемого
аппарата, оснащенного = X + 2 (Y − R Y C ) + 2 (Z − R Z C ) , (1) (1)
R
где X R , Y R , Z R – координаты ракеты, Y C , Z C – координаты воздушной цели (X C =0), причем Y C = V C t,
где X R, Y R, Z R – координаты ракеты, Y C , Z C – координаты воздушной цели (X C=0), причем
оружия с оптическими головками самонаведения матричного типа.
где t – время моделирования.
Y = V t , где t – время моделирования.
C
C
Тогда в соответствии с принятой пространственной схемой взаимного положения ракеты
Описание математической модели

и цели ориентация ГСН с МФПУ в горизонтальной и вертикальной плоскостях определяется
Z
Y
лы наклона линии дал ьности « ракета - цель » р а в н ы θ D D и ϕ D D , а с и г н а л ы р а с с о г л а с о в ан и я п о
лы наклона линии дальности «ракета-цель» равны θ и ϕ , а сигналы рассогласования по
значениями углов θ G и φ G , углы наклона вектора скорости составляют θ M и φ M , углы наклона
Y R
Математическая модель процесса поражения летательного аппарата разработана с ис-
азимуту и углу места равны θΔ θ G θ D θ R
азимуту и углу места равны θΔ и ϕΔ . Обобщенная структурная схема математической моде- и ϕΔ . Обобщенная структурная схема математической моде-
линии дальности «ракета-цель» равны θ D и φ D , а сигналы рассогласования по азимуту и углу
V C
пользованием результатов, полученных в [3, 4]. Относительное движение ракеты и воздуш-
места равны Δθ и Δφ. Обобщенная структурная схема математической модели представлена на
Z C
а
д
и

с
е
р

.
2
.
с
т
п
а
а
р
н
л
ли представлена на рис. 2.
н

е
и
в
л
D р-ц
ной цели Н а рис . 2 и с пользованы с V C е д у ю щ и е обозначе ния : F k k – частота обновления Δφ -
рис. 2. (летательного аппарата) рассматривается в абсолютной системе координат OXYZ с
информа
На рис. 2 использованы следующие обозначения: F – частота обновления информа-
л
V Rn
На рис. 2 использованы следующие обозначения: F k – частота обновления информации
проекциями на горизонтальную XOY и вертикальную YOZ плоскости (рис. 1). Самолет дви-
Δθ
V R

сигналов

и

о
асования
азиму
у

п
т
;
и
)
ц

места
кадров

(

МФПУ
и
рассогл

л
у
значениях
г
у

о
частота
ции о значениях сигналов рассогласования по азимуту и углу места (частота кадров МФПУ);
о значениях сигналов рассогласования по азимуту и углу места (частота кадров МФПУ);
Y C
жется прямолинейно со скоростью V С параллельно оси OY на высоте Z С. Ракета наводится на
φ D
& &
θ
, ϕ – измеренная ГСН угловая скорость вращения линии визирования цели; K G , T
θ , ϕ & – измеренная ГСН угловая скорость вращения линии визирования цели; K , T – , & – измеренная ГСН угловая скорость вращения линии визирования цели; K , T –
G G G – коэф-
φ G φ R
G G
G G
G G
Z R
воздушную цель со скоростью V R. Составляющая вектора Y
фициент усиления и постоянная времени передаточной функции замкнутой петли ГСН; T 1 , T 2 – плос-
X скорости в горизонтальной
коэффициент усиления и постоянная времени передаточной функции замкнутой петли ГСН;
коэффициент у с и л е н и я и постоянная време н и п е р е д а т о ч н о й ф у н к ц и и з а м 0 к н у т ой петли ГСН ;
постоянные времени передаточной функции корректирующего фильтра; K n – навигационная
0
X R
кости равна V Rп. Текущая дальность между ракетой и целью определяется выражением: Y R
н
в
р
е
е
передато

м

и
корректиру

T
–
и
–
п
K
и

T , T – постоянные времени передаточной функции корректирующего фильтра; K – нави-
;
фильтра
щего
T

ю
,
ц

н
ф
у
я
ч
е
ной
н
ы
с
т
н
к
-
о
нави
о
n n
2 2
1 1
постоянная контура самонаведения ракеты; W max – максимальное значение боковой перегруз-
а) горизонтальная плоскость
б) вертикальная плоскость
2
2
2
) , (1)
– максимальное значение боко-
– ования передаточной функции
Z
(Z −
D р-ц ки ракеты; T 3 , ξ – постоянная времени и коэффициент демпфир макси м аль н ое значе н и е боко -
(Y −
гационная постоянная контура самонаведения ракеты;
гационная постоянная контура самонаведения ракеты; WW
) +
Y
=
X +
a
max
m
x
C
C
R
R
R
Рис. 1. Система координат движения ракеты и воздушной цели
ракеты, стабилизированной автопилотом; W g , W v – составляющие боковой перегрузки ракеты
вой перегрузки ракеты; T , ξ – постоянная времени и коэффициент демпфирования переда-T , ξ – постоянная времени и коэффициент демпфирования переда-
вой перегрузки ракеты;
где X R, Y R, Z R – координаты ракеты, Y C , Z C – координаты воздушной цели (X C=0), причем
3 3
по горизонтальной и вертикальной плоскостям; N з – число ЛТЦ в залпе; T з – интервал между
точной функции ракеты, стабилизированной автопилотом; W
точной функции ракеты, стабилизированной автопилотом; W , W – составляющие боковой , W – составляющие боковой
Тогда в соответствии с принятой пространственной схемой взаимного положения ра-
Y = V t , где t – время моделирования. g g v v
C
C
кеты и цели ориентация ГСН с МФПУ в горизонтальной и вертикальной плоскостях опреде-
перегрузки ракеты по горизонтальной и вертикальной плоскостям; N – число ЛТЦ в залпе; N – число ЛТЦ в залпе;
перегрузки ракеты по горизонтальной и вертикальной плоскостям; з з

Z
Y ляется значениями углов θ и ϕ , углы наклона вектора скорости составляют θ и ϕ , уг-
R
G
G
R

число
;

н
-
интервал
N
–
–
е
р
с
T

и
;
и

T T – интервал между моментами отстрела ЛТЦ в залпе; N – число залпов в серии; T – ин-
л
п
а
и
з

в
в
–
о
ж

д
у
стрела
е

в

ЛТЦ
м
от
е
м
а
н
т
м

м
и
о
п
е
з
л
а

с с
з з
с с
Y R
θ R
θ D
–
тервал м е ж д у з а л п а ми в θ G с е р и и ; N п п – число сери й в п о с л е д о в а т е л ь н о с т и ; T п п V C меж -
тервал между залпами в серии; N – число серий в последовательности; T – интервал меж-

интервал
Z C 2
ду последо вательностями .
ду последовательностями.
D р-ц
V C Δφ
V Rn
Δθ V R
Y C φ D
φ G
φ R
Z R
X 0 Y R Y
з
N
Программа отстрела ЛТЦ Программа отстрела ЛТЦ N N c з T з T c T c а) горизонтальная плоскость б) вертикальная плоскость
N з
0
X R
а) горизонтальная плоскость б) вертикальная плоскость
c T
Рис. 1. Система координат движения ракеты и воздушной цели
п
Рис. 1. Система координат движения ракеты и воздушной цели
N
N п
– 224 –
п T
п T

Тогда в соответствии с принятой пространственной схемой взаимного положения ра-
кеты и цели ориентация ГСН с МФПУ в горизонтальной и вертикальной плоскостях опреде-
ляется значениями углов θ и ϕ , углы наклона вектора скорости составляют θ и ϕ , уг-
R
G
R
G

Рис . 2. Обобщенная ст р у кт у рн а я схем а математической м о д е л и
Рис. 2. Обобщенная структурная схема математической модели
2
Модель формирования фоноцелевой обстановки ( блок 1) обеспечивает р а с ч е т теку -
Модель формирования фоноцелевой обстановки (блок 1) обеспечивает расчет теку-
Z
щих координат воздушной цели Y C , Z C и координат точки прицеливания ИК ГСН ракеты в
Y
щих координат воздушной цели C , C и координат точки п р и ц е л и в а н и я И К ГСН ракеты в
соответствии с выражениями:
соответствии с выраж ениями :
3 3