Page 23 - Bahan Ajar Berbasis Flipped Learning pada materi Diferensial

C. Penggunaan Turunan untuk Menentukan Karakteristk Suatu Fungsi
1. Persamaan Garis Singgung pada Kurva

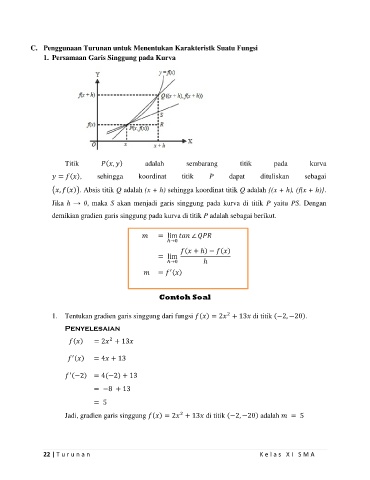
Titik ( , ) adalah sembarang titik pada kurva

= ( ), sehingga koordinat titik P dapat dituliskan sebagai
( , ( )). Absis titik Q adalah (x + h) sehingga koordinat titik Q adalah {(x + h), (f(x + h)}.

Jika h → 0, maka S akan menjadi garis singgung pada kurva di titik P yaitu PS. Dengan

demikian gradien garis singgung pada kurva di titik P adalah sebagai berikut.

= lim ∠
ℎ→0
= lim ( + ℎ) − ( )
ℎ→0 ℎ

′
= ( )

Contoh Soal

1. Tentukan gradien garis singgung dari fungsi ( ) = 2 + 13 di titik (−2, −20).
2
Penyelesaian

( ) = 2 + 13
2
′
( ) = 4 + 13
′
(−2) = 4(−2) + 13
= −8 + 13

= 5

2
Jadi, gradien garis singgung ( ) = 2 + 13 di titik (−2, −20) adalah = 5

22 | T u r u n a n K e l a s X I S M A