Page 29 - Draf 1 - LKS Siswa
P. 29
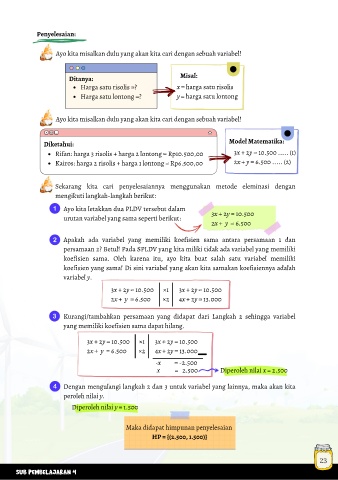
Penyelesaian:
Ayo kita misalkan dulu yang akan kita cari dengan sebuah variabel!
Ditanya: Misal:
Harga satu risolis =? x = harga satu risolis
Harga satu lontong =? y = harga satu lontong
Ayo kita misalkan dulu yang akan kita cari dengan sebuah variabel!
Diketahui: Model Matematika:
Rifan: harga 3 risolis + harga 2 lontong = Rp10.500,00 3x + 2y = 10.500 ..... (1)
Kairos: harga 2 risolis + harga 1 lontong = Rp6.500,00 2x + y = 6.500 ..... (2)
Sekarang kita cari penyelesaiannya menggunakan metode eleminasi dengan
mengikuti langkah-langkah berikut:
Ayo kita letakkan dua PLDV tersebut dalam 3x + 2y = 10.500
urutan variabel yang sama seperti berikut:
2x + y = 6.500
Apakah ada variabel yang memiliki koefisien sama antara persamaan 1 dan
persamaan 2? Betul! Pada SPLDV yang kita miliki tidak ada variabel yang memiliki
koefisien sama. Oleh karena itu, ayo kita buat salah satu variabel memiliki
koefisien yang sama! Di sini variabel yang akan kita samakan koefisiennya adalah
variabel y.
3x + 2y = 10.500 ×1 3x + 2y = 10.500
2x + y = 6.500 ×2 4x + 2y = 13.000
Kurangi/tambahkan persamaan yang didapat dari Langkah 2 sehingga variabel
yang memiliki koefisien sama dapat hilang.
3x + 2y = 10.500 ×1 3x + 2y = 10.500
2x + y = 6.500 ×2 4x + 2y = 13.000
-x = -2.500
x = 2.500 Diperoleh nilai x = 2.500
Dengan mengulangi langkah 2 dan 3 untuk variabel yang lainnya, maka akan kita
peroleh nilai y.
Diperoleh nilai y = 1.500
Maka didapat himpunan penyelesaian
HP = {(2.500, 1.500)}
23
SUB PEMBELAJARAN 4