Page 138 - mathematics first

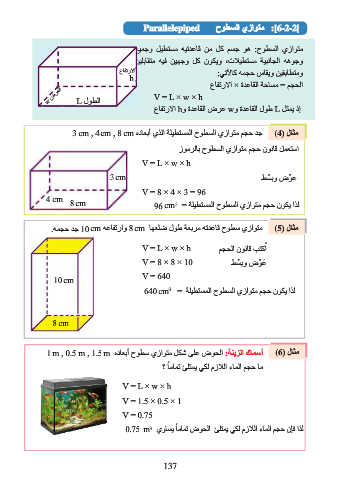
Parallelepiped حوطسلا يزاوتم :]6-2-2[

عيمجو ليطتسم هيتدعاق نم لك مسج وه :حوطسلا يزاوتم
نيلباقتم هيف نيهجو لك نوكيو ،تلايطتسم ةيبناجلا ههوجو

عافترلاا :يتلآاك همجح ساقيو نيقباطتمو
h
عافترلاا × ةدعاقلا ةحاسم = مجحلا
w ضرعلا L لوطلا V = L × w × h

عافترلاا hو ةدعاقلا ضرع wو ةدعاقلا لوط L لثمي ذإ

3 cm , 4 cm , 8 cm هداعبأ يذلا ةليطتسملا حوطسلا يزاوتم مجح دج (4( لاثم

زومرلاب حوطسلا يزاوتم مجح نوناق لمعتسا

V = L × w × h

3 cm طِّ سبو ضِّ وع

V = 8 × 4 × 3 = 96
4 cm
8 cm 96 cm = ةليطتسملا حوطسلا يزاوتم مجح نوكي اذل
3

.همجح دج 10 cm هعافتراو 8 cm اهعلض لوط ةعبرم هتدعاق حوطس يزاوتم (5( لاثم

V = L × w × h مجحلا نوناق بتكا ُ

V = 8 × 8 × 10 طِّ سبو ضِّ وَ ع

V = 640
10 cm
640 cm = ةليطتسملا حوطسلا يزاوتم مجح نوكي اذل
3

8 cm

1 m , 0.5 m , 1.5 m هداعبأ حوطس يزاوتم لكش ىلع ضوحلا :ةنيزلا كامسأ (6( لاثم

ً
؟ امامت ئلتمي يكل مزلالا ءاملا مجح ام

V = L × w × h

V = 1.5 × 0.5 × 1

V = 0.75
ً
0.75 m يواسي امامت ضوحلا ئلتمي يكل مزلالا ءاملا مجح نإف اذل
3

137