Page 108 - 수학(하)
P. 108
예제 05 조합을 이용한 분할과 분배
다음을 구하시오.
1 ]g 학생 8 명을 2 명, 2 명, 4 명의 세 조로 나누는 경우의 수
2 ]g 10 명의 학생이 3 명, 3 명, 4 명씩 짝을 이루어 서로 다른 3 곳의 영화를 관람하는 경우의 수
1 ]g 학생 8 명을 2 명, 2 명, 4 명의 세 조로 나누는 경우의 수는 개념 다지기
1 1
C 2 # 6 C 2 # 4 C4 # ! 2 = 28 # 15 ## 2 = 210 이다. 서로 다른 n 개에서 p 개, q 개, r 개의
1
8
세 묶음으로 나누는 경우의 수
다른풀이 !n 이용
,
1 ]g , pq r 가 모두 다를 경우
! 8 1 유형
! 2 # ! 2 # ! 4 # ! 2 = 210 이다. C p # n- p C q # n- - q C r 06
p
n
,
2 ]g , pq r 중 두 수가 같을 경우
꼼수풀이 C p # C q # C r # 1 조
Y d
p
dd
dddd
C4 # 3 C 1 = 70 # 3 = 210 이다. a 14444444 24444444 3 b k V V b l [ l n n- p n- - q ! 2 합
8
,
8 C4= 70 미리택 3 C1= 3 자동 2 ]g , pq r 가 모두 같을 경우
2 ]g 학생 10 명을 3 명, 3 명, 4 명의 세 조로 나누는 경우의 수는 C p # n- p C q # n- - q C r # 1 ! 3
p
n
C 3 # 7 C 3 # 4 C4 # 1 ! 2 = 120 # 35 ## 1 2 = 210 0 이고
1
10
세 조가 서로 다른 3 곳의 영화를 관람하는 경우의 수는 !3 = 이므로
6
구하는 경우의 수는 곱의 법칙에 의하여 2100 # 6 = 12600 이다.
다른풀이 !n 이용
10 ! 1
학생 10 명을 3 명, 3 명, 4 명의 세 조로 나누는 경우의 수는 # = 2100 이고
334 ! 2
!!!
6
세 조가 서로 다른 3 곳의 영화를 관람하는 경우의 수는 !3 = 이므로
구하는 경우의 수는 곱의 법칙에 의하여 2100 # 6 = 12600 이다.
꼼수풀이
학생 10 명을 3 명, 3 명, 4 명의 세 조로 나누는 경우의 수는 C4 # 5 C 2 = 210 # 10 = 2100 이고
10
6
세 조가 서로 다른 3 곳의 영화를 관람하는 경우의 수는 !3 = 이므로 dddd Y dd ddd
a 14444444 24444444 3 b k V 124444 b l 3 144444 244444 l 3
44
구하는 경우의 수는 곱의 법칙에 의하여 2100 # 6 = 12600 이다. 10 C4= 210 미리택 5 C2= 10 자동
예제 06 순열과 조합을 이용한 함수의 개수
,
,
,
,
,
:
X = " , 12 34, , Y = " , 5678 9, 일 때, 함수 fX $ Y 중
다음 조건을 만족하는 함수의 개수를 구하시오.
y
f yh 2 ]g x < 이면 f x < ^
1 ]g x ! 이면 f x ! ^ y ] g f yh
] g
1 ]g 일대일함수이므로 함수의 개수는 P 4 = 120 이다.
5
5
2 ]g 증가함수이므로 함수의 개수는 C4 = 5 C 1 = 이다.
5
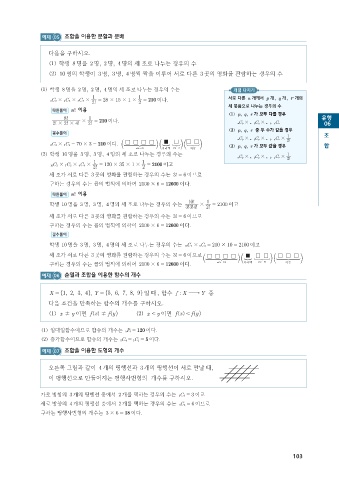
예제 07 조합을 이용한 도형의 개수
오른쪽 그림과 같이 4 개의 평행선과 3 개의 평행선이 서로 만날 때,
이 평행선으로 만들어지는 평행사변형의 개수를 구하시오.
3
가로 방향의 3 개의 평행선 중에서 2 개를 택하는 경우의 수는 C 2 = 이고
3
6
세로 방향의 4 개의 평행선 중에서 2 개를 택하는 경우의 수는 C 2 = 이므로
4
구하는 평행사변형의 개수는 3 # 6 = 18 이다.
103