Page 705 - Microeconomics, Fourth Edition

c16GeneralEquilibriumTheory.qxd 8/16/10 9:14 PM Page 679

16.4 THE EFFICIENCY OF COMPETITIVE MARKETS 679

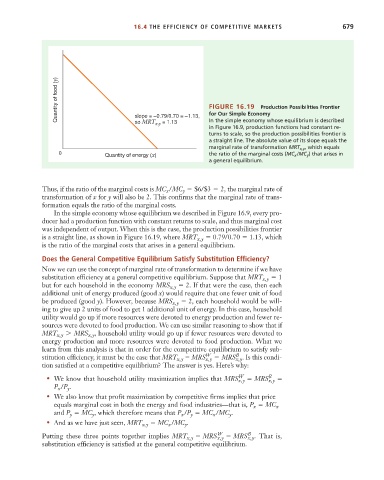
Quantity of food (y) FIGURE 16.19 Production Possibilities Frontier

for Our Simple Economy
slope = –0.79/0.70 = –1.13,
In the simple economy whose equilibrium is described
so MRT
= 1.13
x,y
in Figure 16.9, production functions had constant re-
turns to scale, so the production possibilities frontier is
a straight line. The absolute value of its slope equals the
marginal rate of transformation MRT x,y , which equals
0 Quantity of energy (x) the ratio of the marginal costs (MC x /MC y ) that arises in
a general equilibrium.

Thus, if the ratio of the marginal costs is MC /MC $6/$3 2, the marginal rate of
y
x
transformation of x for y will also be 2. This confirms that the marginal rate of trans-
formation equals the ratio of the marginal costs.
In the simple economy whose equilibrium we described in Figure 16.9, every pro-
ducer had a production function with constant returns to scale, and thus marginal cost
was independent of output. When this is the case, the production possibilities frontier
is a straight line, as shown in Figure 16.19, where MRT x, y 0.79/0.70 1.13, which
is the ratio of the marginal costs that arises in a general equilibrium.

Does the General Competitive Equilibrium Satisfy Substitution Efficiency?
Now we can use the concept of marginal rate of transformation to determine if we have
substitution efficiency at a general competitive equilibrium. Suppose that MRT x, y 1
but for each household in the economy MRS x, y 2. If that were the case, then each
additional unit of energy produced (good x) would require that one fewer unit of food
be produced (good y). However, because MRS x, y 2, each household would be will-
ing to give up 2 units of food to get 1 additional unit of energy. In this case, household
utility would go up if more resources were devoted to energy production and fewer re-
sources were devoted to food production. We can use similar reasoning to show that if
MRT x, y 7 MRS x, y , household utility would go up if fewer resources were devoted to
energy production and more resources were devoted to food production. What we
learn from this analysis is that in order for the competitive equilibrium to satisfy sub-
B
stitution efficiency, it must be the case that MRT x, y MRS W MRS . Is this condi-
x, y
x, y
tion satisfied at a competitive equilibrium? The answer is yes. Here’s why:
• We know that household utility maximization implies that MRS W MRS B x, y
x, y
P /P .
y
x
• We also know that profit maximization by competitive firms implies that price
MC
equals marginal cost in both the energy and food industries—that is, P x x
and P MC , which therefore means that P /P MC /MC .
x
y
x
y
y
y
• And as we have just seen, MRT x,y MC /MC .
y
x
Putting these three points together implies MRT x, y MRS W MRS B x, y . That is,
x, y
substitution efficiency is satisfied at the general competitive equilibrium.