Page 356 - Fiber Optic Communications Fund

Performance Analysis 337

p

p (r) p (r)
0 1

P(0∣1) P(1∣0)

r r
u (T ) T u (T )
0
b
1
b
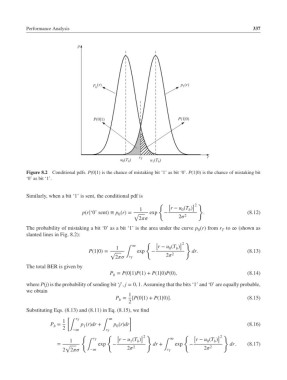
Figure 8.2 Conditional pdfs. P(0|1) is the chance of mistaking bit ‘1’ as bit ‘0’. P(1|0) is the chance of mistaking bit
‘0’ as bit ‘1’.
Similarly, when a bit ‘1’ is sent, the conditional pdf is

2
{ [ ] }
1 r − u (T )
0
b
0
p(r|‘0’ sent) ≡ p (r)= √ exp − 2 . (8.12)
2 2
The probability of mistaking a bit ‘0’ as a bit ‘1’ is the area under the curve p (r) from r to ∞ (shown as
0 T
slanted lines in Fig. 8.2):
2
{ [ ] }
∞ r − u (T )
1 0 b
P(1|0)= √ ∫ exp − 2 dr. (8.13)
2 r T 2
The total BER is given by
P = P(0|1)P(1)+ P(1|0)P(0), (8.14)
b
where P(j) is the probability of sending bit ‘j’, j = 0, 1. Assuming that the bits ‘1’ and ‘0’ are equally probable,
we obtain
1
P = [P(0|1)+ P(1|0)]. (8.15)
b
2
Substituting Eqs. (8.13) and (8.11) in Eq. (8.15), we find
[ ∞ ]
1 r T
P = 2 ∫ −∞ p (r)dr + ∫ p (r)dr (8.16)
b
1
0
2
{ r T { [ ] } ∞ { [ ] }
2
1 r T r − u (T ) r − u (T )
0
1
b
b
= √ ∫ exp − 2 dr + ∫ exp − 2 dr. (8.17)
2 2 −∞ 2 r T 2