Page 56 - FINAL CFA II SLIDES JUNE 2019 DAY 3

LOS 9.l: Explain how to test and correct for seasonality in READING 9: TIME SERIES ANALYSIS
a time-series model and calculate and interpret a
forecasted value using an AR model with a seasonal lag.
Module 9.4: Seasonality

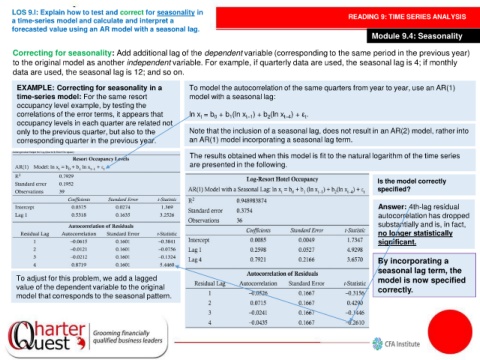
Correcting for seasonality: Add additional lag of the dependent variable (corresponding to the same period in the previous year)
to the original model as another independent variable. For example, if quarterly data are used, the seasonal lag is 4; if monthly
data are used, the seasonal lag is 12; and so on.

EXAMPLE: Correcting for seasonality in a To model the autocorrelation of the same quarters from year to year, use an AR(1)
time-series model: For the same resort model with a seasonal lag:
occupancy level example, by testing the
correlations of the error terms, it appears that ln x = b + b (ln x ) + b (ln x ) + ε .
t–1
1
2
0
t–4
t
t
occupancy levels in each quarter are related not
only to the previous quarter, but also to the Note that the inclusion of a seasonal lag, does not result in an AR(2) model, rather into
corresponding quarter in the previous year. an AR(1) model incorporating a seasonal lag term.
The results obtained when this model is fit to the natural logarithm of the time series
are presented in the following.
Is the model correctly
specified?

Answer: 4th-lag residual
autocorrelation has dropped
substantially and is, in fact,
no longer statistically
significant.

By incorporating a
seasonal lag term, the
To adjust for this problem, we add a lagged model is now specified
value of the dependent variable to the original correctly.
model that corresponds to the seasonal pattern.