Page 36 - FINAL CFA II SLIDES JUNE 2019 DAY 9

LOS 35.e: Describe the process of calibrating a binomial
interest rate tree (BIRT) to match a specific term structure. READING 35: THE ARBITRAGE-FREE VALUATION FRAMEWORK

MODULE 35.2: BINOMIAL TREES, PART 2

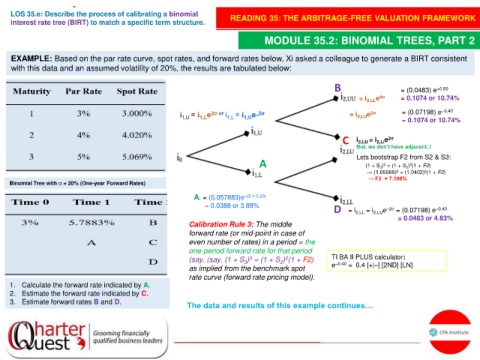
EXAMPLE: Based on the par rate curve, spot rates, and forward rates below, Xi asked a colleague to generate a BIRT consistent
with this data and an assumed volatility of 20%, the results are tabulated below:

B = (0.0483) e +0.80
= i 2,LL e 4σ = 0.1074 or 10.74%

= i 2,LU e 2σ = (0.07198) e +0.40
= 0.1074 or 10.74%

C i 2,LU = i 2,Ll e 2σ
But, we don’t have adjacent..!
Lets bootstrap F2 from S2 & S3:
A (1 + S 3 ) = (1 + S 2 ) (1 + F2)
3
2
→ (1.05069) = (1.0402) (1 + F2)
3
2
→ F2 = 7.198%
Binomial Tree with σ = 20% (One-year Forward Rates)
A. = (0.057883)e –(2 × 0.20)
= 0.0388 or 3.88%
D = i 2,LL = i 2,LU e –2σ = (0.07198) e –0.40
= 0.0483 or 4.83%
Calibration Rule 3: The middle
forward rate (or mid-point in case of
even number of rates) in a period = the
one-period forward rate for that period
3
(say, (say, (1 + S ) = (1 + S ) (1 + F2) TI BA II PLUS calculator:
2
3
2
as implied from the benchmark spot e –0.40 = 0.4 [+|–] [2ND] [LN]
rate curve (forward rate pricing model).
1. Calculate the forward rate indicated by A.
2. Estimate the forward rate indicated by C.
3. Estimate forward rates B and D.
The data and results of this example continues…