Page 45 - FINAL CFA I SLIDES JUNE 2019 DAY 3
P. 45
LOS 10.h: Define the continuous uniform distribution Session Unit 3:
and calculate and interpret probabilities, given a 10. Common Probability Distributions
continuous uniform distribution, p.222
Recall for a continuous uniform distribution, if a < x < b, P(X = x) = 0. Formally stated
• For all a ≤ x1 < x2 ≤ b (i.e., for all x1 and x2 between the boundaries a and b).
• P(X < a or X > b) = 0 (i.e., the probability of X outside the boundaries is zero).
• P(x1 ≤ X ≤ x2) = (x2 – x1)/(b – a). This is probability of outcomes between x1 and x2.
For a continuous uniform distribution, the p of outcomes in a range that is ½ of the whole range is 50% and in ¼ of the of the
whole possible range is 25%.
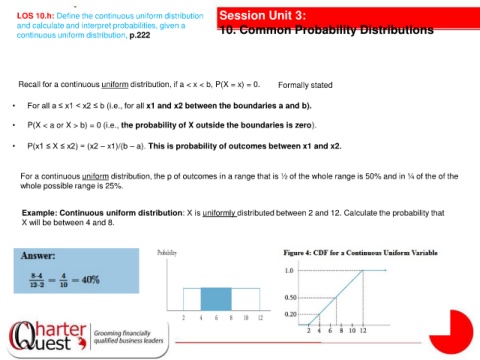
Example: Continuous uniform distribution: X is uniformly distributed between 2 and 12. Calculate the probability that
X will be between 4 and 8.