Page 277 - Services Selection Board (SSB) Interviews

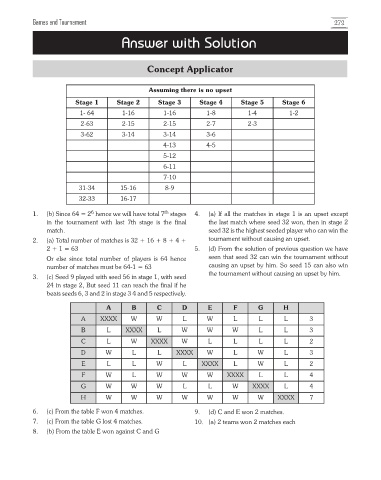
Games and Tournament 273

Answer with Solution

Concept Applicator

Assuming there is no upset
Stage 1 Stage 2 Stage 3 Stage 4 Stage 5 Stage 6
1- 64 1-16 1-16 1-8 1-4 1-2

2-63 2-15 2-15 2-7 2-3
3-62 3-14 3-14 3-6
4-13 4-5
5-12

6-11
7-10
31-34 15-16 8-9
32-33 16-17

th
6
1. (b) Since 64 = 2 hence we will have total 7 stages 4. (a) If all the matches in stage 1 is an upset except
in the tournament with last 7th stage is the final the last match where seed 32 won, then in stage 2
match. seed 32 is the highest seeded player who can win the
2. (a) Total number of matches is 32 + 16 + 8 + 4 + tournament without causing an upset.
2 + 1 = 63 5. (d) From the solution of previous question we have
Or else since total number of players is 64 hence seen that seed 32 can win the tournament without
number of matches must be 64-1 = 63 causing an upset by him. So seed 15 can also win
3. (c) Seed 9 played with seed 56 in stage 1, with seed the tournament without causing an upset by him.
24 in stage 2, But seed 11 can reach the final if he
beats seeds 6, 3 and 2 in stage 3 4 and 5 respectively.

A B C D E F G H
A XXXX W W L W L L L 3
B L XXXX L W W W L L 3

C L W XXXX W L L L L 2
D W L L XXXX W L W L 3
E L L W L XXXX L W L 2
F W L W W W XXXX L L 4

G W W W L L W XXXX L 4
H W W W W W W W XXXX 7

6. (c) From the table F won 4 matches. 9. (d) C and E won 2 matches.
7. (c) From the table G lost 4 matches. 10. (a) 2 teams won 2 matches each
8. (b) From the table E won against C and G