Page 40 - FORMULARIO TRIGONOMETRIA - RAIMONDI

Academia
Formulario de TRIGONOMETRÍA

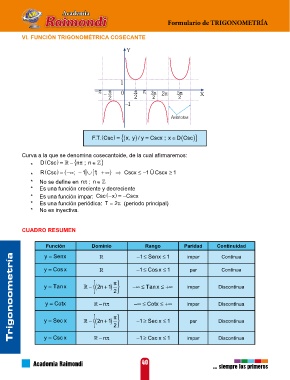
VI. FUNCIÓN TRIGONOMÉTRICA COSECANTE
Y

1
−π π π π
− 0 3π 2π 5π X
2 2 2 2
− 1
Asíntotas

FT Csc..( ) = x y, ( { / ) y = Cscx ; x ∈ D( Csc )}

Curva a la que se denomina cosecantoide, de la cual afirmaremos:

* DCsc) =  ( − n { π ; n ∈ }
(
(
ÛCscx ≥ 1
;
* RCsc) =−∞− ]∪[ ;1 1 + ∞) ⇒ Cscx ≤ −1
* No se define en nπ ; n ∈
* Es una función creciente y decreciente
* Es una función impar: Csc − ( x) =− Cscx
* Es una función periódica: T = 2π (periodo principal)
* No es inyectiva.

CUADRO RESUMEN

Rango
Función x Dominio −≤1 Cosx ≤ 1 Paridad Continuidad
−≤1 Senx
Trigonoometría y = Tan x x  − (2n + ) 1 π } } −∞ ≤ Tanx ≤ +∞ impar Discontinua
y =
Senx
impar

Continua
y = Cos
≤ 1
par
Continua

{
≤ +∞
2
y =
 − nπ
Cotx
−∞ ≤ Cotx
Discontinua
impar
{
π
y = Sec
≤ 1
+ ) 1
−≥1 Secx
 − (2n
par
Discontinua
2
x
y = Csc
Discontinua
40
Academia Raimondi  − nπ −≥1 Cscx ≤ 1 impar ... siempre los primeros