Page 48 - FORMULARIO TRIGONOMETRIA - RAIMONDI

Academia
Formulario de TRIGONOMETRÍA

Y
1 π 5π
5π 1 π Senx > 2 → 6 < x < 6
6 2 6
El conjunto solución general será:
π 5 π
X 6 + 2n π < x < 6 + 2n π ; n ∈
π 5 π
2
2
x+y=1 x ∈ 6 + 2 nπ; 6 + 2 nπ ; n ∈

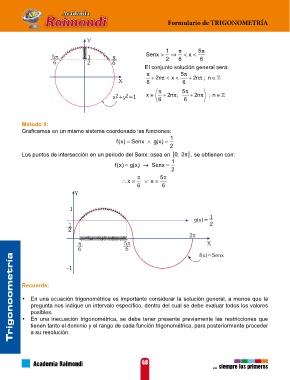
Método II:
Graficamos en un mismo sistema coordenado las funciones:
1
fx() = Senx ∧ gx() =
2
[
Los puntos de intersección en un periodo del Senx: osea en 02; π] , se obtienen con:
1
fx() = gx() → Senx =
2
π 5 π
∴=x ∨ x =
6 6
Y

1

) x ( g = 1
1 2
2
2π
π 5π X
6 6 f(x)=Senx
Trigonoometría Recuerde:
−1

• En una ecuación trigonométrica es importante considerar la solución general, a menos que la
pregunta nos indique un intervalo específico, dentro del cual se debe evaluar todos los valores
posibles.
• En una inecuación trigonométrica, se debe tener presente previamente las restricciones que
tienen tanto el dominio y el rango de cada función trigonométrica, para posteriormente proceder
a su resolución.

Academia Raimondi 48 ... siempre los primeros