Page 41 - Secundaria - Matemáticas 3 - McGraw Hill

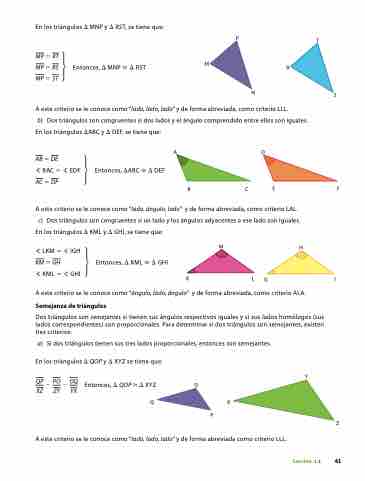
En los triángulos D MNP y D RST, se tiene que:
\ LKM 5 \ IGH KM5GH
\ KML 5 \ GHI
M
H
P
T
MP 5 RT
MP5RS ∂ Entonces,DMNP_DRST M MP 5 ST
R
A este criterio se le conoce como “lado, lado, lado” y de forma abreviada, como criterio LLL.
b) Dos triángulos son congruentes si dos lados y el ángulo comprendido entre ellos son iguales.
En los triángulos DABC y D DEF, se tiene que:
AB 5 DE
\BAC5\EDF ∂ Entonces,DABC_DDEF AC 5 DF
AD
N
S
A este criterio se le conoce como “lado, ángulo, lado” y de forma abreviada, como criterio LAL. c) Dos triángulos son congruentes si un lado y los ángulos adyacentes a ese lado son iguales.
En los triángulos D KML y D GHI, se tiene que:
Semejanza de triángulos
Dos triángulos son semejantes si tienen sus ángulos respectivos iguales y si sus lados homólogos (sus lados correspondientes) son proporcionales. Para determinar si dos triángulos son semejantes, existen tres criterios:
BCEF
∂ Entonces,DKML_DGHI
A este criterio se le conoce como “ángulo, lado, ángulo” y de forma abreviada, como criterio ALA.
a) Si dos triángulos tienen sus tres lados proporcionales, entonces son semejantes. En los triángulos D QOP y D XYZ se tiene que:
QP 2 PO 2 OQ XZ ZY YX
Y
KLGI
Entonces, D QOP L D XYZ O QX
P
A este criterio se le conoce como “lado, lado, lado” y de forma abreviada como criterio LLL.
Lección 1.3 41
Z